
Results on Low Autocorrelation Binary Sequence Problem
Problem Definition
LABS is an NP-hard problem of finding a binary
sequence s={s1,s2,...,sn} with si
Î {-1,
1} that minimizes Energy E(s) or maximizes merit Factor
F(s), where:
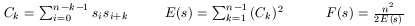
Some example of LABS Instances
LABS is a COP without particular input...
LABS instances are only determined by the size n, the length of the
binary sequence.
For example, with n=3, the best binary sequences are {1,-1,-1},
{-1,1,1}, {-1,-1,1}, or {1,1,-1}, with
E(s) = 1 and
F(s) = 4.5.
Fitness Landscape and Search Trajectory
Analysis
We use the simple Tabu Search algorithm
proposed in
"A Note on Low Autocorrelation Binary Sequences" (Dotu and van
Hentenryck, 2006) to analyze the fitness landscape of LABS instances
and managed to come up with a statistically significantly faster search
strategy. Our tweaked Tabu Search algorithm
(named as TSv7) managed to reach state-of-the-art performance.
TSv7 is faster
than any existing LABS
solvers to date (since April 2008) until someone else develop a
better solver. Please let us know (stevenhalim at gmail dot com) if you
know a better LABS solver.
Note: we can exploit symmetry
property in LABS when sampling the Local Optima. As soon as
we get a LABS solution with objective value equals to the
known optimal values, quickly generate all its symmetries.
Fig 1. As soon as we know one GO (blue circles), immediately
generate all its symmetrical GOs, as shown in Fig 2.
Observable characteristics of
LABS
fitness landscape:
1. Global optima are spread in the fitness landscape, not
clustered!
2. The distance between any local optima (non blue circles) and
the NEAREST global optima is NOT near but falls in
the range of Hamming Distance [n/4 .. 2n/5] bits away. |
 |
|
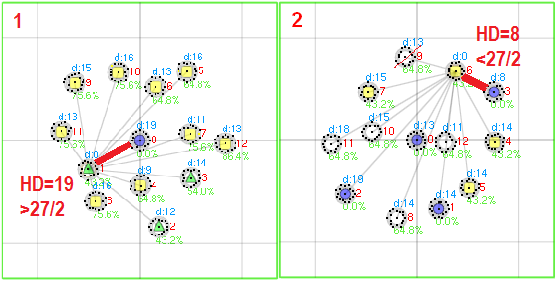
Some observable TS behavior:
3. TS are frequently seen to be near one of the global
optima (near is defined as 20%*n and here n =
27). TS just need to flip 5 more correct bits to reach this
nearest GO, but TS does not do it.
4. Only thousand
iterations later, TS hits this GO.
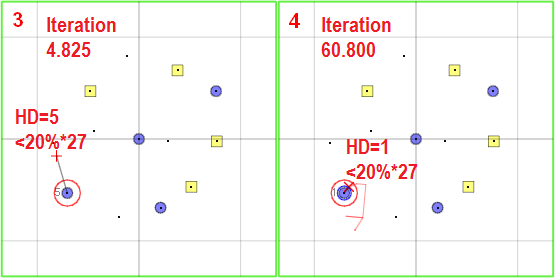
This leads us to
a simple but working insights of making TS do frequent LOCAL
restarts around (but not too close, n/4 bits away) the
current local optima in bid to reach the nearest GO faster!
We call this strategy as TSv7.
|
 |
C++ source code for TSv7 is
available upon request, e-mail stevenhalim at gmail dot com !
Results
In the table below, we list down and
compare the average runtimes in seconds (20 runs) for
these SLS algorithms:
1. TSv0, the original implementation by
(Dotu and van
Hentenryck, 2006)
2. MA_TS, previous state-of-the-art
"A Memetic Algorithm for
the Low Autocorrelation Binary Sequence Problem" (Gallardo et al.,
2007)
3. TSv1, our implementation of the TS algorithm in
(Dotu and van Hentenryck, 2006)
4. TSv7, our improved implementation using the search
strategy mentioned in the FLST analysis above
to get the 1st LABS solution with objective value equals
to the known optimal values when these SLS algorithms are started
from random LABS solution. The LABS instances tested are those with known optimal value
(40
≤ n
≤ 60).
The CPU used for each experiments are listed in the respective
columns.
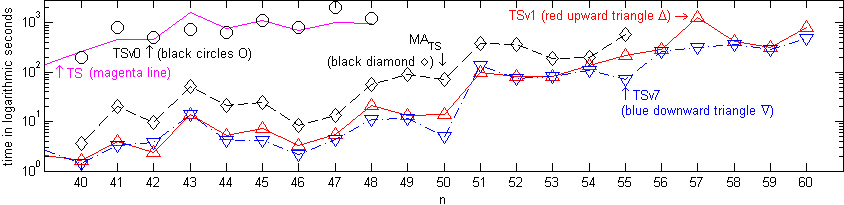
Our TSv1 implementation is
clearly faster than TSv0, the explanation of this phenomenon
are mentioned in our paper. TSv1 and obviously TSv7 are also
faster than MA_TS. As a rough comparison, P4 3 GHz is ~1.25
times faster than P4 2.4 GHz (same architecture); Centrino Duo 2 GHz
should be slightly faster than P4 2.4 GHz (different architecture),
but likely not up to twice or even three times faster; and Centrino
Duo 2 GHz is more or less similar with P4 3 GHz. It can
be seen that TSv1 and TSv7 are still safely faster
than MA_TS after accounting the
possible differences
in computing environment.
Then, the new search strategy employed in
TSv7 also significantly boost its performance on certain
instances compared to TSv1, e.g. n = {45, 48, 50, 55, 57, 60}
(see the green pairs) and slightly faster on almost all instances.
Wilcoxon signed-ranks test on these 21 matched pairs of
average runtimes detects a significant difference between these two
average runtimes data (T = 27.5, p < 0.1), making TSv7
the current state-of-the-art LABS solver.
We have also created a simple
'Run Length to LABS objective value verifier' program
(with its C++ source code). Run "LABS <RLN>" in
command line to check whether the objective values reported in this
table (and the table below for n > 60) are indeed correct.
|
n |
Opt
E(s) |
Opt
F(s) |
TSv0
P4
3 GHz |
MA_TS
P4
2.4 GHz |
TSv1
Centrino
Duo 2 GHz |
TSv7
Centrino
Duo 2 GHz |
One of the
optimal LABS
(in Run Length Notation) |
|
40 |
108 |
7.41 |
260.11 |
3.67 |
1.65 |
1.43 |
111211211343143131312 |
|
41 |
108 |
7.78 |
460.26 |
19.79 |
4.01 |
3.29 |
112112182222111111343 |
|
42 |
101 |
8.73 |
466.73 |
9.76 |
2.36 |
3.76 |
211211211343143131313 |
|
43 |
109 |
8.48 |
1600.63 |
51.56 |
13.90 |
13.65 |
1132432111117212112213 |
|
44 |
122 |
7.93 |
764.66 |
21.56 |
5.15 |
4.17 |
525313113111222111211121 |
|
45 |
118 |
8.58 |
1103.48 |
24.77 |
7.24 |
4.08 |
82121121231234321111111 |
|
46 |
131 |
8.08 |
703.32 |
8.34 |
3.32 |
2.18 |
73235111112132122112121 |
|
47 |
135 |
8.18 |
1005.03 |
13.27 |
5.61 |
4.31 |
111221111111211222224924 |
|
48 |
140 |
8.23 |
964.13 |
56.86 |
20.95 |
11.20 |
1211211222123412381111113 |
|
49 |
136 |
8.83 |
- |
~75^ |
13.45 |
11.66 |
1121212111112131223137333 |
|
50 |
153 |
8.17 |
- |
~50^ |
14.22 |
4.94 |
11211211123111111312224527 |
|
51 |
153 |
8.50 |
- |
~360^ |
99.78 |
137.29 |
23432111141313116212112121 |
|
52 |
166 |
8.14 |
- |
~340^ |
82.58 |
75.89 |
111141111333713221321212121 |
|
53 |
170 |
8.26 |
- |
~190^ |
81.00 |
81.25 |
26522313111221215141112111 |
|
54 |
175 |
8.33 |
- |
~190^ |
138.84 |
110.16 |
121111111222211212141522653 |
|
55 |
171 |
8.85 |
- |
~560^ |
214.73 |
72.50 |
11221221111111121142114A2323 |
|
56 |
192 |
8.17 |
- |
>650 (19)^ |
290.09 |
265.59 |
1112212112311111423211322167 |
|
57 |
188 |
8.64 |
- |
>750 (10)^ |
1294.28 |
323.55 |
11212212211112172111113623233 |
|
58 |
197 |
8.54 |
- |
>640 (13)^ |
409.52 |
360.61 |
2112342311212418312321311111 |
|
59 |
205 |
8.49 |
- |
>610 (18)^ |
315.17 |
295.13 |
6132123121111113112341221121242 |
|
60 |
218 |
8.26 |
- |
>870 (17)^ |
814.65 |
472.38 |
1111112111153117142112412224221 |
Note ^:
The results in
(Gallardo et al., 2007) are displayed as graph for 49 ≤ n
≤ 55 and thus the numbers written here are a kind of
'approximation'. For 56 ≤ n ≤ 60, MA_TS runtimes are incomplete as MA_TS did
NOT actually reach optimal solutions
for some of the 20 runs (the number of runs
that actually reach optimal solution is indicated in
the bracket). Thus, the average runtimes of MA_TS for the last five
instances should be longer than the numbers shown in this table.
Exploring Frontier LABS Instances
(n > 60)
TSv7 is still reasonably fast for
LABS instances up to n
≤ 60,
thus we can use this state-of-the-art
solver to explore frontier LABS instances (n > 60). We run
TSv7
ONE time using initial random seed "1", keep it run until
the time limit is elapsed and report the best found solution. The time limit is computed by TSv7
"runtime predictor" on 40
≤
n
≤
60 (1.03e-5 * 1.34^n), multiplied by "extra" constant
7.0, then divided by 60 to get the runtimes in minutes. However, the predicted runtimes are getting more unbearable as n
gets larger. Therefore, we
limit the runtimes for 71
≤
n ≤ 77 to be 10.0 hours (600 minutes).
These results are obtained using
2.33 GHz Core2 Duo desktop
(our other faster machine).
To date, we are only aware of one
source that published the best known objective values for LABS
instances up to n = 64 (see
"Reliable Cost Predictions for Finding
Optimal Solutions to LABS Problem: Evolutionary and Alternative
Algorithms (Brglez et al., 2003)). TSv7 can replicate the
results for 61 ≤
n ≤ 64 but unable to improve the quality anymore.
Perhaps, these values are indeed optimal. For n > 64, since there is
no basis of comparison yet, we assume that the binary sequences
found by TSv7 are the current best known pseudo-optimal so
far. If any of you who visited this webpage
managed to obtain better results for any of the LABS instances below, please contact us at stevenhalim
at gmail dot com.
|
n |
Best Known so
far (May 2008) |
TSv7
E |
TSv7
F |
TSv7 Runtimes
to get 1st BK |
Max Runtimes
for TSv7 |
Date
Found |
One of the
best found LABS
(in Run Length Notation) |
|
61 |
E = 226 |
226 |
8.23 |
3.35
m |
1.1 h |
21/05/08 |
33211112111235183121221111311311 |
|
62 |
E = 235 |
235 |
8.18 |
8.24
m |
1.5 h |
21/05/08 |
112212212711111511121143111422321 |
|
63 |
E = 207 |
207 |
9.59 |
4.13
m |
2.0 h |
21/05/08 |
2212221151211451117111112323231 |
|
64 |
E = 208 |
208 |
9.85 |
46.62
m |
2.7 h |
21/05/08 |
223224111341121115111117212212212 |
|
65 |
Perhaps -> |
240 |
8.80 |
133.49 m/02.2 h |
3.7 h |
22/05/08 |
132323211111711154112151122212211 |
|
66 |
Perhaps -> |
265 |
8.22 |
186.08 m/03.1 h |
4.9 h |
22/05/08 |
24321123123112112124123181111111311 |
|
67 |
Perhaps -> |
241 |
9.31 |
245.92 m/04.1 h |
6.6 h |
22/05/08 |
12112111211222B2221111111112224542 |
|
68 |
Perhaps -> |
250 |
9.25 |
393.95 m/06.6 h |
8.8 h |
22/05/08 |
11111111141147232123251412112221212 |
|
69 |
Perhaps -> |
274 |
8.69 |
493.55 m/08.2 h |
11.8 h |
25/05/08 |
111111111141147232123251412112221212 |
|
70 |
Perhaps -> |
295 |
8.31 |
744.17 m/12.4 h |
15.8 h |
26/05/08 |
232441211722214161125212311111111 |
|
71 |
Perhaps -> |
275 |
9.17 |
467.33 m/07.8 h |
10.0 h |
28/05/08 |
241244124172222111113112311211231121 |
|
72 |
Perhaps -> |
300 |
8.64 |
144.26 m/02.4 h |
10.0 h |
29/05/08 |
1111114111444171151122142122224222 |
|
73 |
Perhaps -> |
308 |
8.65 |
73.44 m/01.2 h |
10.0 h |
29/05/08 |
1111112311231122113111212114171322374 |
|
74 |
Perhaps -> |
349 |
7.85 |
13.93 m/00.2 h |
10.0 h |
27/05/08 |
11321321612333125111412121122511131111 |
|
75 |
Perhaps -> |
341 |
8.25 |
479.40 m/08.0 h |
10.0 h |
30/05/08 |
12122132121211211111131111618433213232 |
|
76 |
Perhaps -> |
338 |
8.54 |
378.30 m/04.6 h |
10.0 h |
30/05/08 |
111211112234322111134114212211221311B11 |
|
77 |
Perhaps -> |
366 |
8.10 |
235.45 m/03.9 h |
10.0 h |
31/05/08 |
111111191342222431123312213411212112112 |
References
These results are reported in more
details in our publications (download the local copy of those papers
here):
-
S. Halim, R. Yap, F. Halim. Engineering Stochastic
Local Search for the Low Autocorrelation Binary Sequence Problem.
In Principles and Practice of Constraint Programming (CP
2008, Sydney, Australia, September 14-18, 2008): to appear
|