Important: Please read Lab Guidelines before you continue.
This lab consists of 3 exercises. You are required to submit 2 exercises. If you submit 3 exercises, the best 2 out of 3 exercises will be used to determine your attempt mark.
The main objective of this lab is on the use of one-dimensional arrays to solve problems.
The maximum number of submissions for each exercise is 15.
If you have any questions on the task statements, you may post your queries on the relevant IVLE discussion forum. However, do not post your programs (partial or complete) on the forum before the deadline!
Important notes applicable to all exercises here:
This problem is adopted from National Software Competition 2006 for junior college students. (Copyright: NSC 2006.)
Professor Robert A.J. Matthews of the Applied Mathematics and Computer
Science Department at the University of Aston in Birmingham, England,
has recently described how the positions of stars across the night sky
may be used to deduce a surprisingly accurate value of
p. This result followed from the
application of certain theorems in number theory.
Here, we don't have the night sky, but we can use the same theoretical basis to form an estimate for p.
Given any pair of positive integers chosen from a large set of random numbers, the probability that these two integers having no common factor other than one is 6/p2.
For example, using this small set of five numbers {2, 3, 4, 5, 6}, there are 10 pairs that can be formed: (2,3), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6), (4,5), (4,6) and (5,6). Six of these 10 pairs - (2,3), (2,5), (3,4), (3,5), (4,5), and (5,6) - have no common factor other than one. Using the ratio of the counts as the probability we have:
6/p2 = 6/10. Hence the estimated value of p is 3.1623, correct to four decimal places.
As another example, given this set of 10 numbers {32391, 14604, 3902, 153, 292, 12382, 17421, 18716, 19718, 19895}, there are 24 pairs that have no common factor other than one, among a total of 45 pairs. We have:
6/p2 = 24/45. Hence the estimated value of p is 3.3541, correct to four decimal places.
Write a program estimatePi.c that reads in a positive integer n representing the size of the list, followed by n unique positive integers (representing the random numbers). Your program then prints out an estimate value for p (using double type) accurate to 4 decimal places. The set contains at most 50 unique positive integers.
You will be given two files: gcd.h which you need to include in your program, and gcd.o which you need to compile together with your program. The gcd.o object file contains the GCD function which you are required to use in your program.
Sample runs using interactive input (user's input shown in blue; output shown in bold purple). Note that the first two lines (in green below) are commands issued to compile and run your program on UNIX.
You would need to use the -lm option in gcc if you use some math function in your program.
$ gcc -Wall -lm estimatePi.c gcd.o -o estimatePi $ estimatePi 3 7 4 10 Estimated pi = 3.0000
Sample run #2:
5 2 3 4 5 6 Estimated pi = 3.1623
Sample run #3:
10 32391 14604 3902 153 292 12382 17421 18716 19718 19895 Estimated pi = 3.3541
The time here is an estimate of how much time we expect you to spend on this exercise. If you need to spend way more time than this, it is an indication that some help might be needed.
Given a list, a k-interval subsequence is a sublist where each element in the subsequence is k positions away from the next element in the subsequence.
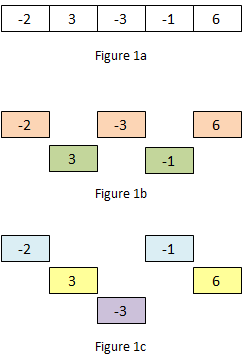
For example, Figure 1a shows a list with 5 elements {-2, 3, -3, -1, 6}. Figure 1b shows the two 2-interval subsequences {-2, -3, 6} and {3, -1}. Figure 1c shows the three 3-interval subsequences {-2, -1}, {3, 6}, and {-3}. In general, there are k k-interval subsequences derivable from a list. You should have noticed that the 1-interval subsequence is the list itself.
Your task is to find the maximum sum of a k-interval subsequence among all k-interval subsequences. You are to report the solution subsequence: its sum, its interval k, and its starting position.
For the above example, all the k-interval subsequences and their respective sums are listed below:
Hence, the solution is the 3-interval subsequence starting at position 1 with a sum of 9.
There might be more than one subsequence with the maximum sum. For example, given the list {1, 5, 5 -6, -2, -2}, there are two subsequences with the maximum sum of 5:
You should report the former as its value of k (the interval) is smaller.
A skeleton program is given. You are to complete the given function
void sum_subsequence(int arr[], int size, int ans[])
You are NOT to change the function header given above, or marks will be deducted.
As the task is to find 3 values: the maximum sum, the interval, and the starting position, the ideal approach is to use address parameters or structure. However, we have not covered either of these topics yet. Hence, for the moment, we will use a 3-element integer array ans to hold the values, which are incidentally all integers (hence we can use an array):
You may assume that there is at least one element and at most 10 elements in the list.
Sample runs using interactive input (user's input shown in blue; output shown in bold purple). Note that the first two lines (in green below) are commands issued to compile and run your program on UNIX.
$ gcc -Wall subsequence.c -o subsequence $ subsequence Enter number of elements: 1 Enter 1 element: 123 Max sum 123 of 1-interval subsequence starting at position 0.
Second sample run:
$ subsequence Enter number of elements: 5 Enter 5 elements: -2 3 -3 -1 6 Max sum 9 of 3-interval subsequence starting at position 1.
Third sample run:
$ subsequence Enter number of elements: 6 Enter 6 elements: 1 5 5 -6 -2 -2 Max sum 5 of 4-interval subsequence starting at position 2.
The time here is an estimate of how much time we expect you to spend on this exercise. If you need to spend way more time than this, it is an indication that some help might be needed.
This exercise is tedious to code. Please brace yourself for long hours of preparation, coding and testing!
In the far far land of Maruku, there lives a population of optimistic frogs. Overly optimistic actually. Their life philosophy revolves around the idea of being forward looking. They believe that there is only one way in life, which is to move forward. Frogs who turn back are condemned in the society.
One fine day, two clans of frogs meet at the bridge of Marukunan River. The problem is, they are on different ends trying to cross the bridge. A nearby tourist commented, "Oh no, there's no way they can cross the bridge!" while another shouted, "Use your forward thinking to leap across all obstacles!".
The frogs stood there for a long time, thinking of a way to cross the bridge without dishonoring their family until a CS1010 student came by and said "Oh, I think they can cross it alright. It's just a matter of how many jumps will they need to take."
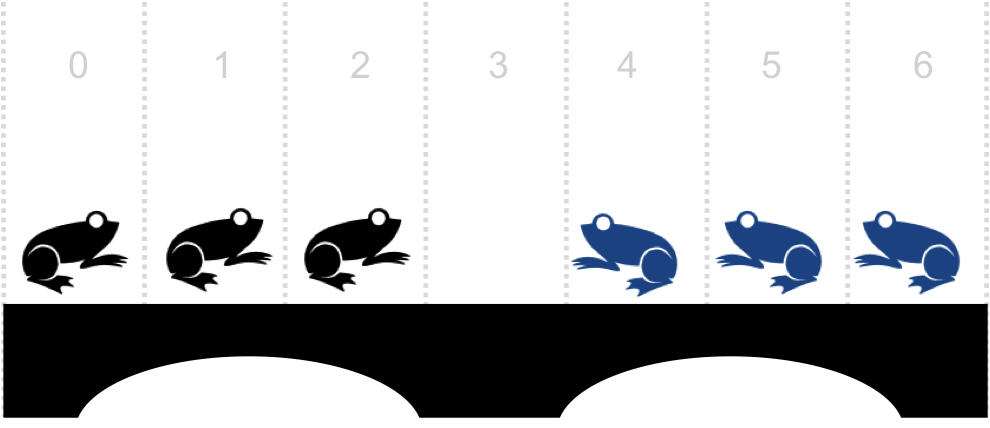
Figure 2. Frogs on the bridge
Write a program frogs.c to simulate a way for the frogs to cross the bridge. To simulate this, you are to write an integer array to represent the bridge and each element will represent the one frog or an empty space.
Each frog can only jump into the space in front of it, or jump over one frog into the space after that frog.
Your program should take in the length of a bridge (array), and the frogs and space (1, 0 or -1) at each position of the bridge. The user will then be able to move a frog to jump to the empty space directly in front of it OR to jump over a frog to the empty space behind the latter.
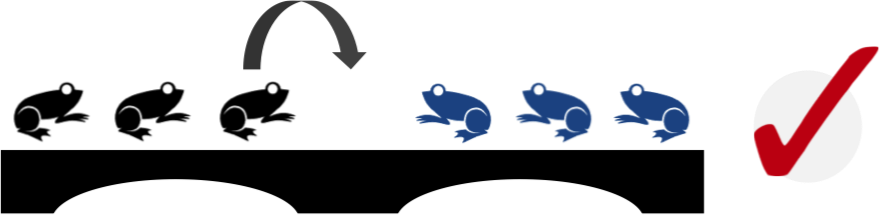
Figure 3-1. A frog can jump into empty space in front of it
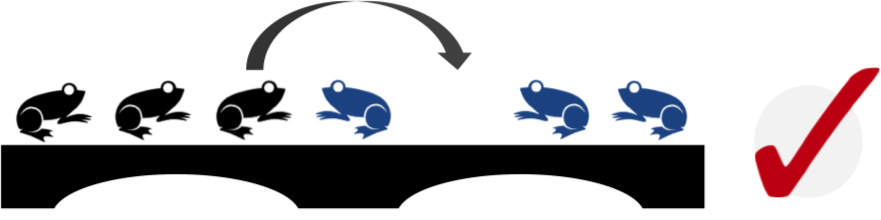
Figure 3-2. A frog can jump over the frog in front of it to the empty space behind the latter
Figure 3-3. A frog can only jump into an empty space
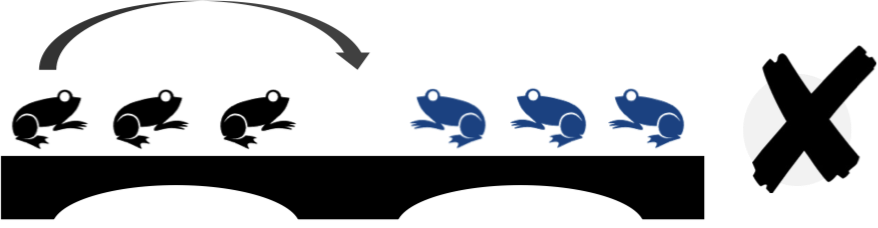
Figure 3-4. A frog cannot jump so far!
Figure 3-5. A frog cannot jump backwards
Finally, your program should output when the game has ended. A game has ended if there is no possible jumps or all the frogs have successfully crossed the bridge. If they are successful, your program should output the number of jumps the frogs took to cross.
Figure 4-1. The frogs are stuck! Game over.
Figure 4-2. All the frogs have crossed the river!
You can be assured that the length of the bridge will not exceed 1000 and there is only one empty space on the bridge.
Sample run using interactive input (user's input shown in blue; output shown in bold purple). Note that the first two lines (in green below) are commands issued to compile and run your program on UNIX.
Initialising the array:
$ gcc -Wall frogs.c -o frogs $ frogs Please enter the length of the bridge: 7 Please insert frog at position 0: 1 Please insert frog at position 1: 1 Please insert frog at position 2: 1 Please insert frog at position 3: 0 Please insert frog at position 4: -1 Please insert frog at position 5: -1 Please insert frog at position 6: -1
The above inputs represents Figure 2.
Write a function to print out the current state of bridge and its positions:
Position: 0 1 2 3 4 5 6 Bridge: 1 1 1 0 -1 -1 -1
Sample run (move frog)#1:
Move the frog at position: 2 Position: 0 1 2 3 4 5 6 Bridge: 1 1 0 1 -1 -1 -1
Frog at position 2 can jump into the empty space at position 3.
Sample run (move frog)#2:
Move the frog at position: 4 Position: 0 1 2 3 4 5 6 Bridge: 1 1 -1 1 0 -1 -1
Frog at position 4 can jump over frog at position 3 to the empty space in position 2.
Sample run (move frog)#3:
Move the frog at position: 1 Invalid move!
Frog at position 1 can only jump to the right, but there is no empty space.
Sample run (move frog)#4:
Move the frog at position: 4 Invalid move!
Position 4 is empty, therefore it's an invalid move.
The program comes to an end when all frogs have crossed the bridge or when there is no more possible moves. Sample outcome #1:
Position: 0 1 2 3 4 5 6 Bridge: -1 -1 -1 0 1 1 1 Congratulations! The frogs took 15 jumps to cross the bridge!
Sample outcome #2:
Position: 0 1 2 3 4 5 6 Bridge: 1 1 -1 1 -1 -1 0 Oh no! It seems like the two clans of frogs are stuck!
The time here is an estimate of how much time we expect you to spend on this exercise. If you need to spend way more time than this, it is an indication that some help might be needed.
The deadline for submitting all programs is 1 October 2016, Saturday, 12 noon. Late submission will NOT be accepted.