The planning of such a round robin tournament can become a time consuming task, especially if there are many additional constraints. Friar Tuck is designed to solve such a planning task. It provides graphical input facilities for many kinds of constraints and solves the resulting tasks using a technique called constraint programming.

To see how Friar Tuck works, go to the menu "Demos" on the top and choose one of the items. Follow the instructions in the window that will pop up.
You may want to play with your own example. For this, go to the menu "File" on top and select "New Task". Enter a "number of teams", say 5, and a "number of rounds", say 1 (each team plays each other team once; single round robin). Now, you can click on "Timetables" on the left and search for a timetable by clicking "Next" in section "Planning". You can look at the resulting timetable by clicking on "Current Show" in section "Display".
First, the user specifies a task, including all the constraints that belong to the sport tournament at hand. To find a timetable, Friar Tuck needs to find patterns. Patterns are sequences of home and away (and bye for odd number of teams) flags. From the generated patterns, a pattern set is constructed. A pattern set consists of as many patterns as there are teams. Based on such a pattern set, Friar Tuck can construct a timetable.
These four phases are represented by the fields Friar Tuck displays messages related to the phases in the corresponding field. Clicking on the field opens a control panel for the corresponding phase on the right hand side of the main window. To get familar with this interface and with the problem solving process, you may want to load the demo "DRR 3" (click on "Demos" in the top menu and select "DRR 3"). Now go through the phases Patterns, Pattern Sets and Timetables, clicking on the buttons in sections "Planning" and "Display".
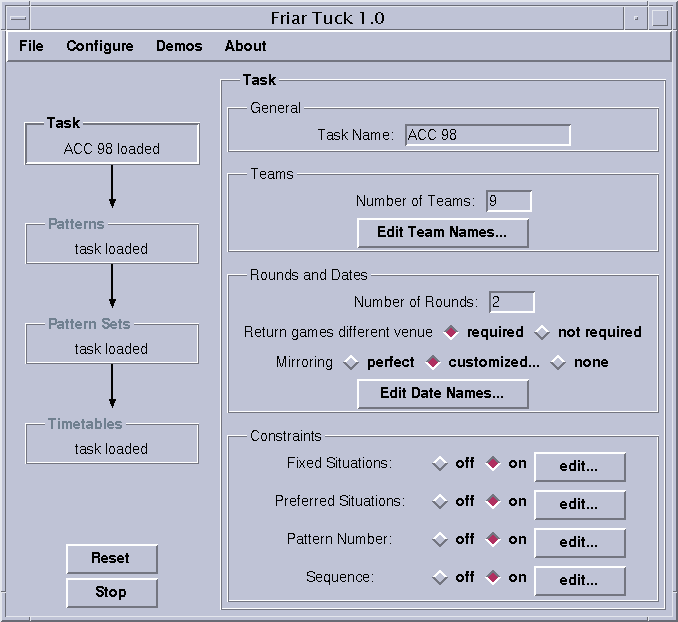
The specification of a task is explained using the ACC 98/99 example, a difficult tournament planning problem described by G. NEMHAUSER AND M. TRICK: Scheduling a major college basketball conference, Operations Research 46(1), 1998.
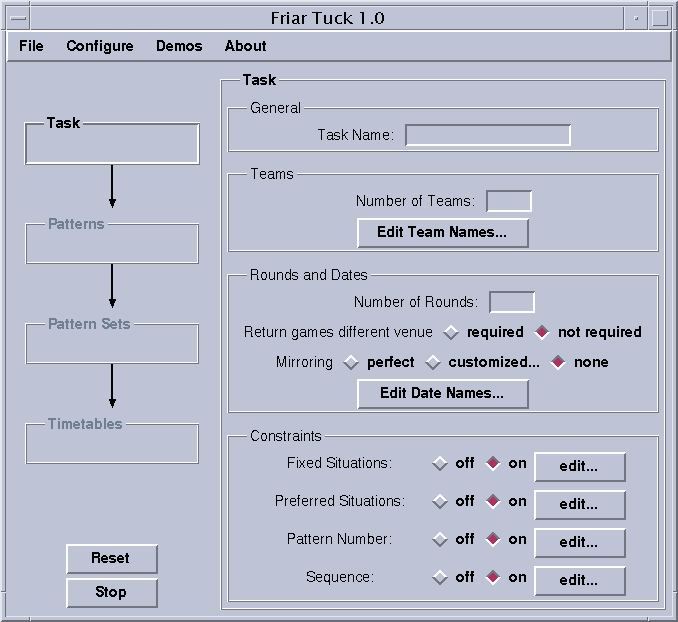
The control panel for task entry appears on the right after clicking on the field "Task" on the left.
The Number of Teams is the most important data for planning. If this number is even, every team plays on every date of the round robin. If this number is odd, all teams except one play on every date. The team that does not play at a given date is said to have a "bye" on that date.
The Number of Rounds is the number of times that two given teams play against each other. If this number is 1, we have a single round robin; if it is 2, we have a double round robin; and if it is bigger than 2, we say it is a multiple round robin. The number of dates for the tournament is equal to the number of rounds times the number of teams if the number of teams is odd, and the number of teams minus one if the number of teams is even.
In a double round robin, each team plays each other team twice. The first match is called "first leg", the second is called "return match". You can decide whether first leg and return match should have different venue. This is useful for example to satisfy fans, because if return matches have different venue, the fans will get to see their team play at home against every other team exactly once.
Also specific to double round robins is mirroring. Mirroring allows to fix the dates in which return games occur. Perfect mirroring means that the overall plan has two mirrored halves. For example, in a perfectly mirrored double round robin with 4 teams (6 dates), the matches occurring in the first date reappear in the fourth date, the matches of the second reappear in the fifth and the matches of the third reappear in the sixth. Other mirroring schemes can be entered by clicking on "customized...". The choice "none" means that return matches are not date-wise mirrored; for two matches that happen in a given date, the corresponding return matches could be carried out at different dates.
Team names as well as date names can be edited for display in windows and web pages.
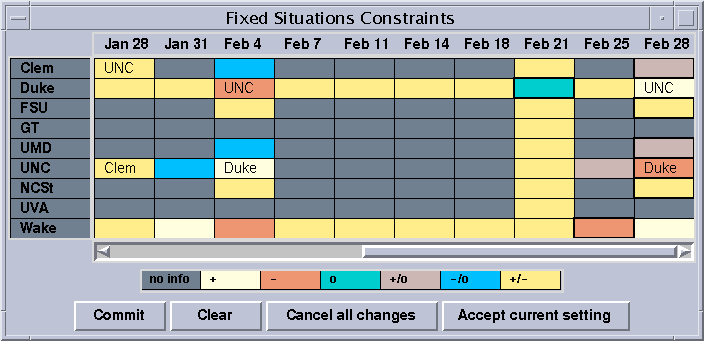
The result after propagation of the "fixed situations" constraints in the ACC 98 example looks like this.
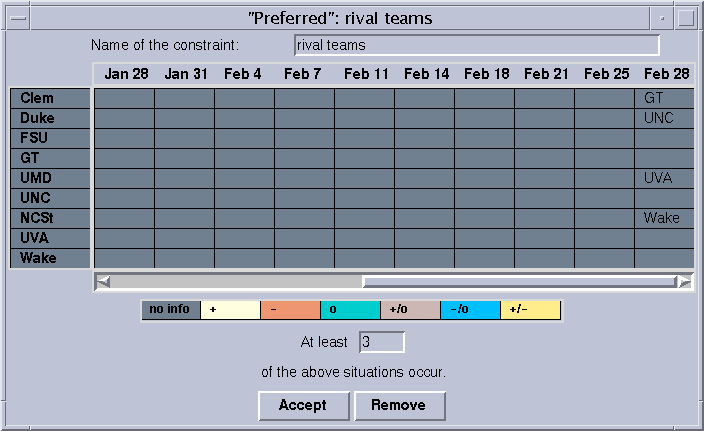
For example, the constraint that three out of four given pairings must occur in the last round of the ACC 98 example is specified like this.
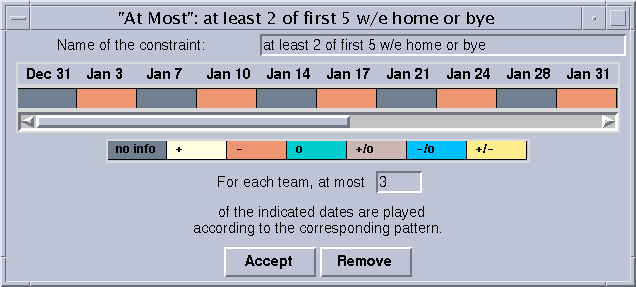
"Balanced Home/Away" allows to specify whether each team should have exactly as many home matches as it has away matches.
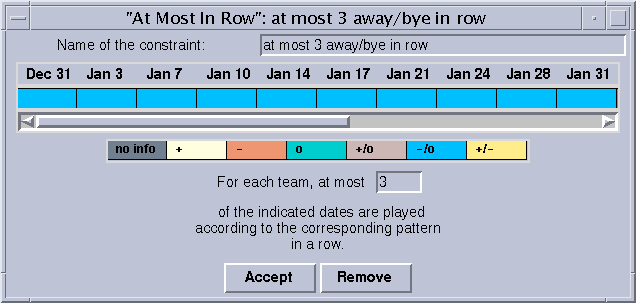
For example, this is how you can specify that there should be at most 3 away games or byes in a row.
For single round robins and perfectly mirrored double round robins, "Minimizing Breaks" allows to minimize the number of sequences of two home matches or two away matches (breaks) in a row within each round. For odd numbers of teams, such breaks can be avoided altogether, for even number of teams, the number of breaks can be reduced to the number of teams minus two per round. Minimizing breaks greatly reduces the number of pattern sets and feasible timetables, but leads to efficient computation of timetables even for a large number of teams (up to 30 teams on a PC with usual configuration).
After clicking on "Patterns" on the left, the control panel for pattern generation appears on the right. Patterns can be generated and displayed separately or all at once.
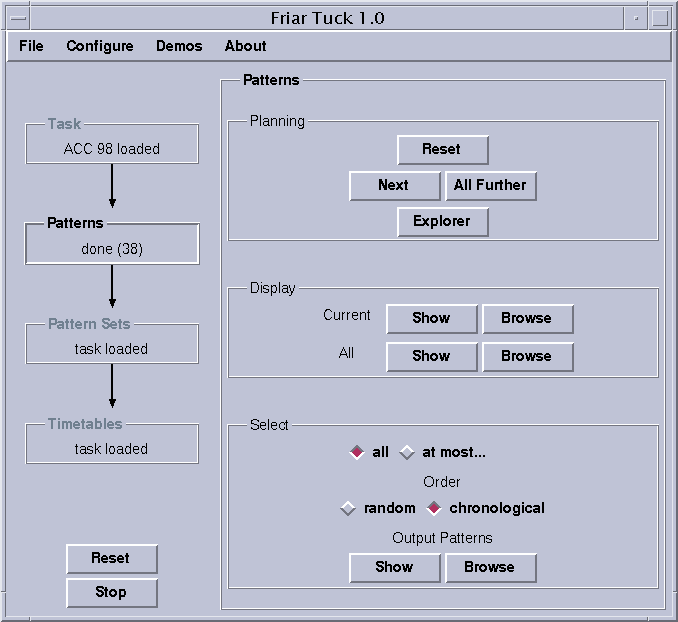
You should aim for a number below 100 patterns. If necessary, add pattern constraints to the task. If the number of patterns is higher than 100, it is crucial to restrict the number of patterns used by pattern set generation. This is done using the at most... entry. The patterns used for pattern set generation can be chosen randomly from the computed pattern or in the order in which they are generated (chronological). Most of the time randomly works better than chronological. Of course whenever not all patterns are used for pattern set generation, there may be feasible timetables that are not found by Friar Tuck.
In the ACC 98 example, there are 38 patterns and thus no restriction is necessary.
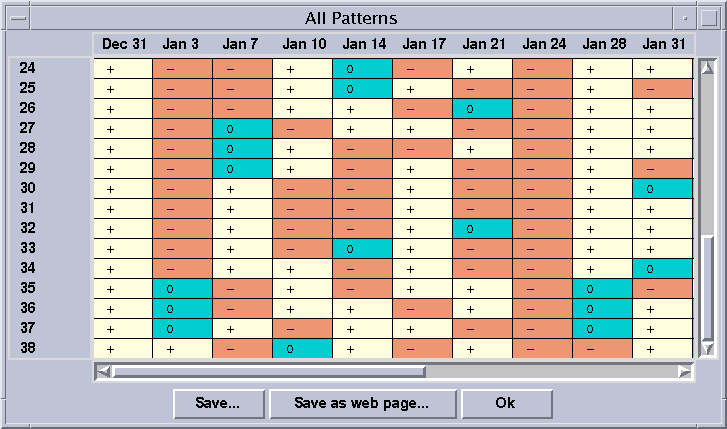
A pattern set for ACC 98 looks like this.

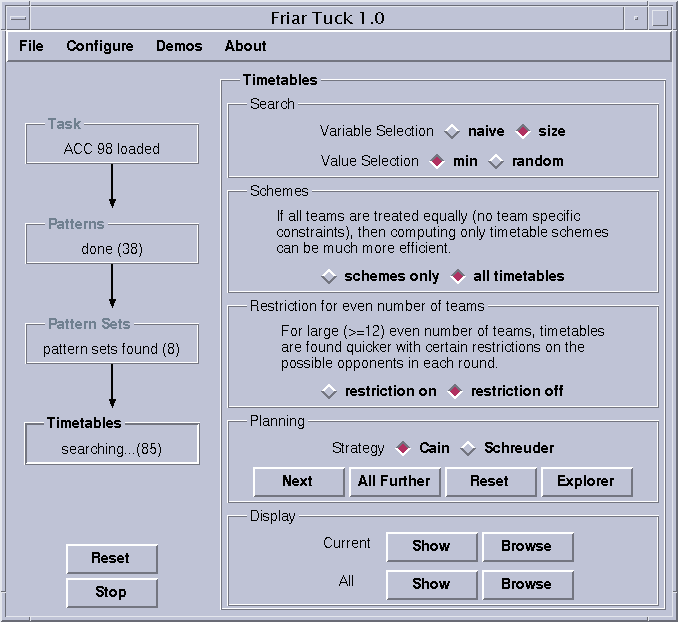
In section "Search" two parameters used by the constraint programming engine can be changed. Play with these parameters if nothing else helps for finding timetables within reasonable time.
If there are no team specific constraints, every team can be treated equally by the search. The switch "schemes only" will generate much fewer timetables (usually also much faster), each of which stands for all possible permutations of teams.
If the number of teams is even, a special restriction can be added that will result in much faster search. Unfortunately, this restriction may not be able to find some timetables which are feasible according to the task description.
In the "Planning" section, two different constraint-based methods can be chosen. Cain's method assigns teams to patterns in the given pattern set first, before the matches are decides, whereas Schreuder's method computes so-called placeholder timetables each row of which is then assigned to a team. Usually Cain's method performs better. However, occasionally Schreuder's method is faster.
The resulting timetables can be displayed like this.

Using the button "Save as web page", a timetable can be saved in HTML format which can be displayed using your favorite web browser like this. Use your web browser for printing and communicating timetables.
If you use Friar Tuck to solve large or difficult tournament planning problems, you may notice that your computer becomes slow because Friar Tuck consumes too much of the main memory of your computer. You can use the Oz Panel to set up memory consumption of Friar Tuck. For this, click on the menu "Configure" on the top of the main window and select "Panel". In this panel, you can monitor the memory consumption and - if necessary - reduce the maximal size of the memory used by Friar Tuck to less than half of the main memory available on your computer.