
The objective is to assign the ships to ports on a one-to-one basis in such a way as to minimize the total cost for all four shipments. Use the Hungarian method to solve this problem.
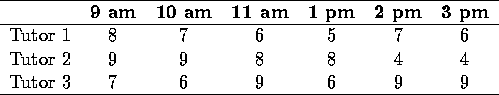
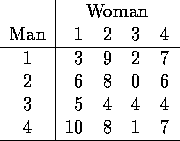
 be a measure of the
mutual pleasure the ith man and the jth woman derive, on the average
per day spent together on a scale of one to ten. This measure is summarized
in the following matrix
be a measure of the
mutual pleasure the ith man and the jth woman derive, on the average
per day spent together on a scale of one to ten. This measure is summarized
in the following matrix
- Let
 be the fraction of his time/day that man i spends with
woman j.
Suppose that the men and
women do nothing but spend their time together.
Formulate a linear program that will help these men and women to
find out how much time that they should spend with each other to
maximize their total happiness.
be the fraction of his time/day that man i spends with
woman j.
Suppose that the men and
women do nothing but spend their time together.
Formulate a linear program that will help these men and women to
find out how much time that they should spend with each other to
maximize their total happiness. - Explain why the optimal solution in part (a) will have four
 and twelve
and twelve
 Since the optimal solution requires that each
person spend all his or her time with one person of the opposite sex, this
result is often referred as the Marriage Theorem.
Since the optimal solution requires that each
person spend all his or her time with one person of the opposite sex, this
result is often referred as the Marriage Theorem. - Determine the marriage partner of each person.
- What can you say about the solution of the linear program if you replace the max in the objective function by min.