Querying Constraint Databases

Participants: Guozhu Dong, Leonid Libkin, Limsoon Wong

Background

A relational database is traditionally formalized as a collection of finite relations. But this has limitation in some applications such as representing and querying spatial data. Thus, Kanellakis, Kuper, and Revesz in their famous PODS'90 paper introduce the idea of constraint databases and query languages for dealing with this type of data and queries. The original idea of constraint query languages is that quantifiers in a query can range over (say) the entire universe of real numbers, as opposed to only over those real numbers that occur in the underlying database. That is, constraint query languages permit the use of quantifiers under the ``natural domain semantics'' interpretation, while traditional database query languages interpret quantifiers strictly under the ``active domain semantics''. This ability to quantify over an infinite universe gives rise to two problems: (i) Queries now may have input/output that are infinite, so how would you represent them? (ii) How would you compute the queries if variables range over an infinite universe? These problems are solved by choosing an infinite universe with an underlying structure that allows an infinite set (on the universe) to be finitely representable and effectively computable. In this project, we study issues relating to constraint query languages where the underlying universe is the real closed field. The constraint query languages we study include extensions (with infinite sets and quantification over the real closed field) of relational calculus, SQL, and nested relational calculus. Towards the end of this project, we also venture into the ``embedded'' model theory of infinitary logics.

Achievements

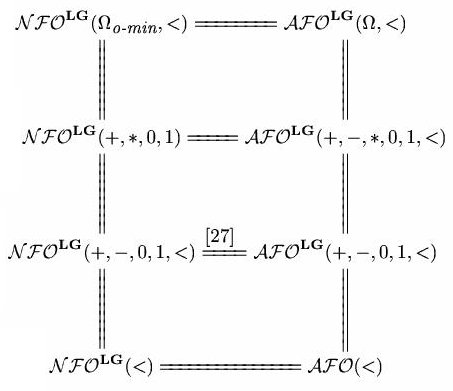
We established a number of powerful ``collapse'' results. For example, the class of generic boolean queries expressible in relational calculus augmented with constraints on any o-minimal structure (such as the real closed field) coincides with the class of queries expressible in the relational calculus. We proved such results for both the natural and active-domain semantics.
Consequently, the relational calculus augmented with polynomial inequalities expresses the same classes of generic boolean queries under both the natural and active-domain semantics. The famous Kanellakis Conjecture---that recursive queries such as parity test and transitive closure cannot be expressed in the relational calculus augmented with polynomial inequality constraints over the reals---followed as a corollary.
We proposed a model and query language frNRC for finitely representable nested relations by extending NRC(=) to deal with possibly infinite relations that are finitely representable by using real polynomial constraint theory. We showed that frNRC has the conservative extension property. We also showed that it is effectively computable, has NC data complexity, and is equivalent to the relational calculus augmented with real polynomial constraints modulo encoding of input/output.

The research above also got us interested in ``embedded'' finite model theory in the context of query languages...

One of the interesting questions we studied was: Could we find a powerful logic into which aggregate queries could be easily embedded, and whose properties could be analyzed so that bounds for query languages could be derived? We found one: L_aggr, which defines every arithmatic operation and every aggregate function. We showed that L_aggr has locality properties in the sense of Haif and of Gaifman. Thus L_aggr has the bounded degree property.
We further defined a query language NRL_aggr on nested relations that models both aggregation and grouping features of SQL. We showed that queries from flat tables to flat tables in NRL_aggr can be translated into L_aggr. Thus NRL_aggr enjoys locality properties and bounded degree property. This implies that SQL augmented with every possible aggregate functions, including those that are non-computable, still cannot express generic recursive queries such as transitive closure.

Selected Publications

Michael Benedikt, Guozhu Dong, Leonid Libkin, Limsoon Wong. Relational Expressive Power of Constraint Query Languages. Proceedings of 15th ACM Symposium on Principles of Database Systems, Montreal, Canada, 5--16, June 1996.
Michael Benedikt, Guozhu Dong, Leonid Libkin, Limsoon Wong. Relational Expressive Power of Constraint Query Languages. Journal of the ACM, 45(1):1--34, January 1998. PS
Leonid Libkin, Limsoon Wong. Unary Quantifiers, Transitive Closure, and Relations of Large Degrees. Proceedings of 15th Symposium on Theoretical Aspects of Computer Science, Paris, France, 183-193, February 1998. PS
Lauri Hella, Leonid Libkin, Juha Nurmonen, Limsoon Wong. Logics with Aggregate Operators. Proceedings of 14th IEEE Symposium on Logic in Computer Science, Trento, Italy, July 1999, 35--44. PS
Elisa Bertino, Barbara Catania, Limsoon Wong. Finitely Representable Nested Relations. Information Processing Letters, 70(4):165--173, 1999. PS
Lauri Hella, Leonid Libkin, Juha Nurmonen, Limsoon Wong. Logics with Aggregate Operators. Journal of the ACM, 48(4):880--907, 2001. PS
Leonid Libkin, Limsoon Wong. Lower Bounds for Invariant Queries in Logics with Counting. Theoretical Computer Science, 288(1):153--180, 2002. (Reviewed invited paper.) PS

Acknowledgements

This project is supported in part by the Japan Real World Computing Partnership (Wong).

Last updated: 10/8/06, Limsoon Wong.