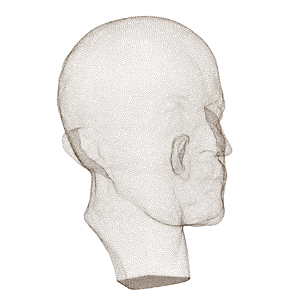
Surface Reconstruction by Layer Peeling

Chi-Wan Lim and Tiow-Seng Tan

National University of Singapore

School of Computing

Abstract

Given an input point cloud P in R³, this paper proposes a novel algorithm to identify surface neighbors of each point p Î P respecting the underlying surface S, and then to construct a piecewise linear surface for P. The algorithm utilizes the simple k-nearest neighborhood in constructing local surfaces. It makes use of two concepts: a local convexity criterion to extract a set of surface neighbors for each point, and a global projection test to determine an order for the reconstruction. Our algorithm not only produces a topologically correct surface for well-sampled point sets, but also adapts well to handle under-sampled point sets. Furthermore, the computational cost of the algorithm increases almost linearly in the size of the point cloud. It thus scales well to deal with large input point sets.

　

CR Categories: I.3.5 [Computer Graphics]: Curve, surface, solid, and object representations.

Keywords: Surface Reconstruction, Mesh Generation, Geometric Modeling, Sampling, Scattered data

Full Text: The Visual Computer, vol. 22, no. 9--11, September 2006, pp. 593--603. (Special Issue: The 2006 Pacific Graphics, 11-13 October, Taipei, Taiwan). Powerpoint Presentation (28M)

Video Download: LayerPeeling.mov (22.1M)

Executable (version 1.0, 3 Dec 2006): click here to download page.

PhD thesis. (6M), presentation (25.5M)

　

More Results

　

We have implemented our algorithm on a Pentium IV 3.0GHz, 4GB DDR2 RAM and nVidia GeForce 6600 with 256MB DDR3 video memory.

Part 1: Regularly Sampled Point Sets

In this first part, we apply our Layer Peeling Algorithm on various point sets.

　

Igea (134345 Points)	Reconstructed Surface

Lion (183408 Points)	Reconstructed Surface

Maxplanck (49132 Points)	Reconstructed Surface

RockerArm (40177 Points)	Reconstructed Surface

Part 2: Under-Sampled Point Sets

In this second part, we regularly down-sampled the point sets and test our algorithm on it.

　

　

Armadillo Full Point Set (172974 Points)	Layer Peeling Reconstruction (5787 Points)

Bunny Full Point Set (35947 Points)	Layer Peeling Reconstruction (1220 Points)

Hipbone Full Point Set (139205 Points)	Layer Peeling Reconstruction(1964 Points)

Horse Full Point Set (48484 Points)	Layer Peeling Reconstruction (3042 Points)

Santa Full Point Set (75781 Points)	Layer Peeling Reconstruction (1098 Points)

Part 3: Irregularly Sampled Point Sets

In this final part, we demonstrate the flexibility of our Layer Peeling Algorithm on three irregularly sampled point sets.

Buddha (543652 Points)	Dragon (437626 Points)	Lucy (262909 Points)

The point models were obtained from the follow URL:

http://www.cs.princeton.edu/gfx/proj/sugcon/models/

http://www.cyberware.com

http://graphics.stanford.edu/data/3Dscanrep/

　

Acknowledgements This research is supported by the National University of Singapore under grants R-252-000-216-112 and R-252-000-254-112.

The authors can be contacted at:  limchiwa @ gmail.com,  and  tants @ comp.nus.edu.sg

ã11 October 2006, 3 December 2006, 28 Feb 2008, 13 March 2008, Computer Graphics Research Laboratory, School of Computing, National University of Singapore.

　

This document, layerPeeling.html, has been accessed 152 times since 25-Jun-24 11:57:13 +08. This is the 2nd time it has been accessed today.

A total of 97 different hosts have accessed this document in the last 149 days; your host, 18.220.6.168, has accessed it 1 times.

If you're interested, complete statistics for this document are also available, including breakdowns by top-level domain, host name, and date.