Selection and Repetition II
Lab #4 (AY2007/8 Semester 1)
Date of release: 18 September 2007, Tuesday, 23:59.
Submission deadline: 3 October 2007, Wednesday, 23:59.
School of Computing, National University of Singapore

0 Introduction

This lab contains three exercises. You are to submit only the first two exercises. Exercise 3 is for your own practice and it will not be graded.

You are advised to review the material covered in chapters 1 through 6 and read Programming Style, Design and Marking Guidelines before attempting this lab assignment. You should not use syntax or constructs not covered in lectures; you shouldn't need to and may even be penalized for doing so (if the objective of the assignment is undermined).

A word of advice: Code incrementally. This is even more important now than before as your program gets longer. Don't try to finish all parts of a program then compile it. Write your program in bits and pieces and compile frequently. Try to maintain a compilable program even while you are working on it. Submitting a compilable program that partially works is better than submitting an un-compilable one. This last point especially applies to the programming exams. Seriously, code incrementally.

The following topics have not been covered and hence you should not use them (if you are in doubt whether you can use certain features not mentioned below and are not yet covered in class, please consult your discussion leader or lecturer first):

• Arrays
• Exceptions
• Recursion
• Inheritance and polymorphism

You may assume that all input data are correct.

You should use Scanner class on System.in for input and System.out for output in your programs, unless otherwise stated.

Your last output statement should be a println and not print.

Test your programs thoroughly with your own input data before you submit to CourseMarker. Do not use CourseMarker as a debugging tool. For this lab, the number of submissions is set to 10. Only your last submission will be graded.

Make good use of the 1-week recess for revision.

In general, the expected time to complete a lab assignment (including all graded exercises) is between 3 to 5 hours. You should aim not to spend more than 5 hours. It might be difficult at first, but it should get easier as you gain experience. Make that your target.

1 Exercise 1: Remainder (20%)

1.1 Learning objectives

• Selection and repetition statements
• Solving a simple mathematical puzzle

1.2 Task

This question appears in a Primary 5 Mathematics paper:

There is a number less than 100, where

• Dividing it by 3 yields remainder 1
• Dividing it by 4 yields remainder 2
• Dividing it by 5 yields remainder 3
• Dividing it by 6 yields remainder 4

What is the number?

For this exercise, you are going to write a program Remainder.java to read in two positive integers m and n (m < n), and find the number of values in the range [m,n] that satisfy the above 4 criteria. For example, between 100 and 1000 inclusive, there are 15 values that satisfy the above 4 criteria: 118, 178, 238, 298, 358, 418, 478, 538, 598, 658, 718, 778, 838, 898 and 958. So the answer your program should produce is 15.

1.3 Sample runs

Sample run using interactive input (user's input shown in blue; output shown in bold purple):

$ javac Remainder.java
$ java Remainder
Enter m and n: 1 50
0

Another sample run:

$ java Remainder
Enter m and n: 100 1000
15

1.4 Submission

Submit your program Remainder.java through CourseMarker.

1.5 Important notes

• You should have a method solvePuzzle(int, int) which computes the answer and returns it to the caller.
  
  
• This is a very simple exercise and we hope that every student is able to complete it within half an hour.
  
  

2 Exercise 2: Bisection Method (80%)

2.1 Learning objectives

• Selection and repetition statements.
• Floating-point numbers.
• DecimalFormat class.

2.2 Task

Numerical analysis is an important area in computing. One simple numerical method we shall study here is the Bisection method, which computes the root of a continuous function. The root, r, of a function f is a value such that f(r) = 0.

How does bisection method work? It is best explained with an example. Given this polynomial p(x) = x³ + 2x² + 5, we need to first provide two endpoints a and b such that the signs of p(a) and p(b) are different. For example, let a=-3 (hence p(a)=-4) and b=0 (hence p(b)=5).

The principle is that, the root of the polynomial (that is, the value r where p(r) = 0) must lie somewhere between a and b. So for the above polynomial, the root r must be somewhere between -3 and 0.

This is achieved as follows. The bisection method finds the midpoint m of the two endpoints a and b, and depending on the sign of p(m) (the function value at m), it replaces one of the two endpoints with m, and repeats the process, until the difference between the two endpoints falls within a threshold, that is, when they become very close to each other, or, when the midpoint is the root itself. For the former case, we shall set the threshold to 0.0001 for this exercise.

Figure 1 below shows the two endpoints a (-3) and b (0), their midpoint m (-1.5), and the function values at these 3 points: p(a) = -4, p(b) = 5, p(m) = 6.125.

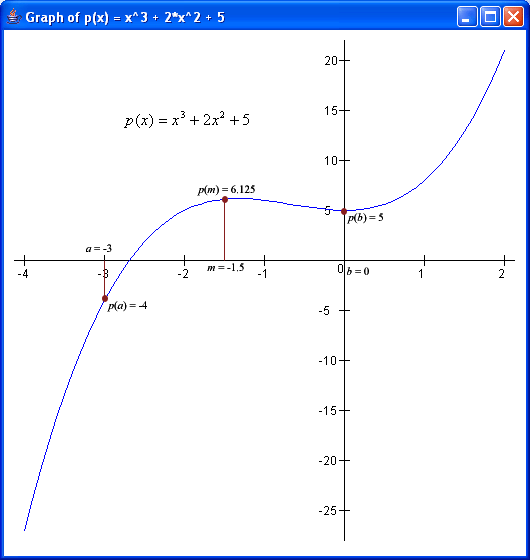
Figure 1. Graph of p(x) = x³ + 2x² + 5

The following table illustrates the iterations in the process. The end-point that is replaced by the mid-point value computed in the previous iteration is highlighted in pink background.

iteration	endpoint a	endpoint b	midpoint m	function value p(a)	function value p(b)	function value p(m)
1	-3.000000	0.000000	-1.500000	-4.000000	5.000000	6.125000
2	-3.000000	-1.500000	-2.250000	-4.000000	6.125000	3.734375
3	-3.000000	-2.250000	-2.625000	-4.000000	3.734375	0.693359
4	-3.000000	-2.625000	-2.812500	-4.000000	0.693359	-1.427002
5	-2.812500	-2.625000	-2.718750	-1.427002	0.693359	-0.312714
6	-2.718750	-2.625000	-2.671875	-0.312714	0.693359	0.203541
7	-2.718750	-2.671875	-2.695312	-0.312714	0.203541	-0.051243
8	-2.695312	-2.671875	-2.683594	-0.051243	0.203541	0.076980
9	-2.695312	-2.683594	-2.689453	-0.051243	0.076980	0.013077
10	-2.695312	-2.689453	-2.692383	-0.051243	0.013077	-0.019031
11	-2.692383	-2.689453	-2.690918	-0.019031	0.013077	-0.002964
12	-2.690918	-2.689453	-2.690186	-0.002964	0.013077	0.005059
13	-2.690918	-2.690186	-2.690552	-0.002964	0.005059	0.001048
14	-2.690918	-2.690552	-2.690735	-0.002964	0.001048	-0.000958
15	-2.690735	-2.690552	-2.690643	-0.000958	0.001048	0.000045
16	-2.690735	-2.690643	-2.690689	-0.000958	0.000045	-0.000456

Hence the root of the above polynomial is -2.690689 (because the difference between a and b in the last iteration is smaller than the threshold 0.0001), and the function value at that point is -0.000456, close enough to zero.

(Some animations on the bisection method can be found on this website: Bisection method. Look at the first one.)

Write a program Bisection.java that asks the user to enter the integer coefficients (c3, c2, c1, c0) for a polynomial of degree 3: c3×x³ + c2×x² + c1×x + c0. It then asks for the two endpoints, which are real numbers. You may assume that the user enters a continuous function with a real root. You may use the double data types for real numbers. To simplify matters, you may also assume that the two endpoints the user entered have function values that are opposite in signs.

Real numbers are to be displayed accurate to 6 decimal digits (see output in sample runs below).

2.3 Sample runs

Sample run using interactive input (user's input shown in blue; output shown in bold purple). Only the last 2 lines shown in bold purple are what your program needs to produce. The iterations are shown here for your own checking only.

The sample run below shows the output for the above example. Note that the iterations end when the difference of the two endpoints is less than 0.0001, and the result (root) is the midpoint of these two endpoints.

$ javac Bisection.java
$ java Bisection
Enter coefficients (c3,c2,c1,c0) of polynomials: 1 2 0 5
Enter endpoints a and b: -3 0
#1: a = -3.000000; b = 0.000000; m = -1.500000
     p(a) = -4.000000; p(b) = 5.000000; p(m) = 6.125000
#2: a = -3.000000; b = -1.500000; m = -2.250000
     p(a) = -4.000000; p(b) = 6.125000; p(m) = 3.734375
#3: a = -3.000000; b = -2.250000; m = -2.625000
     p(a) = -4.000000; p(b) = 3.734375; p(m) = 0.693359
#4: a = -3.000000; b = -2.625000; m = -2.812500
     p(a) = -4.000000; p(b) = 0.693359; p(m) = -1.427002
#5: a = -2.812500; b = -2.625000; m = -2.718750
     p(a) = -1.427002; p(b) = 0.693359; p(m) = -0.312714
(... omitted for brevity ...)
#15: a = -2.690735; b = -2.690552; m = -2.690643
     p(a) = -0.000958; p(b) = 0.001048; p(m) = 0.000045
#16: a = -2.690735; b = -2.690643; m = -2.690689
     p(a) = -0.000958; p(b) = 0.000045; p(m) = -0.000456

root = -2.690689
p(root) = -0.000456

The second sample run below shows how to find the square root of 5. For polynomial where there are more than one real root, only one root needs to be reported.

$ java Bisection
Enter coefficients (c3,c2,c1,c0) of polynomials: 0 1 0 -5
Enter endpoints a and b: 1 3
#1: a = 1.000000; b = 3.000000; m = 2.000000
     p(a) = -4.000000; p(b) = 4.000000; p(m) = -1.000000
#2: a = 2.000000; b = 3.000000; m = 2.500000
     p(a) = -1.000000; p(b) = 4.000000; p(m) = 1.250000
(... omitted for brevity ...)
#16: a = 2.236023; b = 2.236084; m = 2.236053
     p(a) = -0.000201; p(b) = 0.000072; p(m) = -0.000065

root = 2.236053
p(root) = -0.000065

2.4 Submission

Submit your program Bisection.java through CourseMarker.

2.5 Important notes

• Array is strictly disallowed for this exercise.
  
  
• You are reminded that only two lines of output (those shown in bold purple in the sample runs above) are the required output. Your program is not to display the iterations in your output.
  
  
• Note that your program will be tested with a number of test data.

3 Exercise 3: MasterMind® (0%)

3.1 Learning objectives

• Creating some Java classes
• Instantiating objects
• Constructor, accessor and mutator methods
• Overriding method toString
• Selection and repetition statements
• Developing a game

3.2 Task

You are given these 2 codes:

• Peg.java (full code; not to be modified)
• FourPegs.java (partial code)

In the game of MasterMind®, a secret code of 4 pegs are hidden from the player's view. Pegs are in six different colours: Red ('R'), Green ('G'), Blue ('B'), Yellow ('Y'), Cyan ('C'), and Magenta ('M'). The program Peg.java defines the Peg class, which implements the colours by using a character to represent each colour ('R', 'G', 'B', 'Y', 'C', and 'M').

The player tries to break the secret code by making guesses, where each guess consists of 4 pegs. The player is awarded 'sinks' and 'hits' points as follows. A sink point is awarded if a peg in the guess matches the colour of the corresponding peg in the same position in the secret code. A hit is awarded if a peg in the guess matches only the colour of some peg in the secret code, but not the position. A sink takes precedence over a hit; that is, if a peg has already contributed to a sink point, it should not be used to compare for a hit.

The game ends when the player gets 4 sinks, or when he/she has made the maximum number of attempts.

There are two versions of the game. In one version, the secret code may contain two or more pegs of the same colour. In another version, no duplicate colour is allowed. We shall implement the first version here.

Refer to the sample runs below for some examples. Note that the secret code is deliberately displayed for you to check the correctness of sinks and hits awarded.

Please take note of the following:

1. The file Peg.java is given to you. It is not to be modified. You may not need to use all the methods in the Peg class in your other programs.
   
   
2. You are to complete and submit FourPegs.java. The partial code is given to you.
   
   
   • You should not modify the methods that have been completed for you: the 3 constructors, setColour and getColour.
     
     
   • You are to complete the toString, countSinks and countHits methods. You may change the signatures of countSinks and countHits to your liking.
     
     
   • You may add other methods deemed necessary.
   
   
3. You are to write and submit MasterMind.java that implements the MasterMind game. Note that:
   
   
   • The maximum number of attempts for the player to make guesses is 10.
     
     
   • This program may call any method in the FourPegs class, but it may not call any method in the Peg class.
     
     
   • You may add other methods deemed necessary.
     
     
   • You are to read a string of 4 characters from the player. If the string has length other than 4, you should ask the player to re-enter, as shown in the second sample run below.
     
     
   • You may assume that the characters in the string entered by the player are valid characters that represent the colours. A FourPeg object representing the player's guess should be created from the data in the string.
     
     
   • The String method charAt(int) might be handy. You may refer to the API Specification for charAt(int).
     
     
   • Hint: In generating the secret code, you may use an appropriate method in the Random class to generate 4 integers each in the range [0, 5], and map each number to a corresponding colour. You may refer to the API Specification for Random class.
     (You may choose not to follow the hint and do it your own way.)

3.3 Sample runs

Sample run using interactive input (user's input shown in blue; output shown in bold purple):

$ javac Peg.java
$ javac FourPegs.java
$ javac MasterMind.java
$ java MasterMind
                        Secret code: G R R C
Enter your guess: BGRM

                          Guess #01: B G R M      Sinks = 1; Hits = 1
Enter your guess: YCCY

                          Guess #02: Y C C Y      Sinks = 0; Hits = 1
Enter your guess: RRCC

                          Guess #03: R R C C      Sinks = 2; Hits = 1
Enter your guess: BBMY

                          Guess #04: B B M Y      Sinks = 0; Hits = 0
Enter your guess: CGCG

                          Guess #05: C G C G      Sinks = 0; Hits = 2
Enter your guess: CCCG

                          Guess #06: C C C G      Sinks = 0; Hits = 2
Enter your guess: CGRR

                          Guess #07: C G R R      Sinks = 1; Hits = 3
Enter your guess: RRCG

                          Guess #08: R R C G      Sinks = 1; Hits = 3
Enter your guess: RGCR

                          Guess #09: R G C R      Sinks = 0; Hits = 4
Enter your guess: CRRG

                          Guess #10: C R R G      Sinks = 2; Hits = 2

Sorry you didn't get it. The secret code is G R R C.
Hope you have enjoyed the game. Bye!

Another sample run:

$ java MasterMind
                        Secret code: B M Y R
Enter your guess: GG
Enter your guess: GGRRR
Enter your guess: GGRR

                          Guess #01: G G R R      Sinks = 1; Hits = 0
Enter your guess: MMMY

                          Guess #02: M M M Y      Sinks = 1; Hits = 1
Enter your guess: BMBY

                          Guess #03: B M B Y      Sinks = 2; Hits = 1
Enter your guess: BMYC

                          Guess #04: B M Y C      Sinks = 3; Hits = 0
Enter your guess: BMYR

                          Guess #05: B M Y R      Sinks = 4; Hits = 0

Congratulations!
Hope you have enjoyed the game. Bye!

3.4 Submission

You do not need to submit this exercise.

3.5 Important notes

• Ensure that the outputs of your program comform to the format of the sample outputs given.
  
  
• As the topic on arrays has not been covered, we suggest that you do not use array in this assignment. Although as a result some parts of the code will be repetitive and long, it is still bearable, since the number of pegs is only 4. You could treat the array version as an enhancement later, and write it on your own.
  However, if some of you insist on using array, we will allow you to do so, without extra credit. But you might need to modify certain part of the program FourPegs.java that is given to you.
  
  
• You may further enhance your MasterMind program by adding graphics to it. Since students always tell us that doing assignments for grading takes away the fun, we shall let you work on this enhancement for your own pleasure and at your own leisure. :) ☺
  
  

4 Deadline

The deadline for handing in all programs is 3 October 2007, Wednesday, 23:59. (Yes, you are given more than two weeks for this lab assignment - thanks to the 1-week recess!) Late submissions will NOT be accepted.

Start early. Do not wait till the eleventh hour and rush to meet the deadline.

• 0 Introduction
  
  
• 1 Exercise 1: Remainder (20%)
  • 1.1 Learning objectives
  • 1.2 Task
  • 1.3 Sample runs
  • 1.4 Submission
  • 1.5 Important notes
  
  
• 2 Exercise 2: Bisection Method (80%)
  • 2.1 Learning objectives
  • 2.2 Task
  • 2.3 Sample runs
  • 2.4 Submission
  • 2.5 Important notes
  
  
• 3 Exercise 3: MasterMind (0%)
  • 3.1 Learning objectives
  • 3.2 Task
  • 3.3 Sample runs
  • 3.4 Submission
  • 3.5 Important notes
  
  
• 4 Deadline