Research
Overview
My research interests lie at the intersection of information theory, machine learning, and high-dimensional statistics, with ongoing areas of interest including the following:
- Information-theoretic understanding of statistical inference and learning problems
- Adaptive decision-making under uncertainty (e.g., Bayesian optimization, bandits)
- Theory and algorithms for large-scale inference and learning (e.g., group testing, graph learning)
If you have been admitted to the NUS PhD program and are looking for a supervisor, feel free to email me to arrange a meeting. Other prospective PhD applicants are also welcome to get in touch, but I apologize that I may not reply to most enquiries. Admission to NUS can be done through the Department of Computer Science, the Department of Mathematics, or the Institute of Data Science.
If you would like to apply for a post-doc or research assistant position, please send me your CV and an outline of your research interests. Applicants should have a strong track record in an area related to my research interests, such as machine learning, information theory, statistics, statistical signal processing, or theoretical computer science.
Research Group
- Ivan Lau (PhD Student)
- Chenkai Ma (PhD Student)
- Arpan Losalka (post-doc)
- Recep Can Yavas (post-doc)
- Yash Pote (post-doc)
- Hoang Ta (post-doc)
- Daniel McMorrow (Research Assistant)
Former postdocs: Lan Truong (U. Essex), Qiaoqiao Zhou (Southeast U.), Daming Cao (NUIST), Zhaoqiang Liu (UESTC), Thach Bui (VNU-HCM), Prathamesh Mayekar (Propheus), Yan Hao Ling (NTU)
Former RAs: Anamay Chaturvedi (ISTA), Selwyn Gomes (UCSD), Hangdong Zhao (U. Wisconsin-Madison), Mayank Shrivastava (UIUC)
Research Funding
- (Nov. 2024 - Nov. 2027) Adaptive and Resource-Efficient Sequential Decision-Making Algorithms, AI Visiting Professorship ($2.87M, w/ Kevin Jamieson)
- (Oct. 2024 - Oct. 2029) Statistical Estimation and Learning with 1-bit Feedback, NUS Presidential Young Professorship ($320k)
- (March 2023 - March 2026) Safety and Reliability in Black-Box Optimization, MoE Academic Research Fund (AcRF) Tier 1 ($250k)
- (May 2019 - May 2024) Robust Statistical Model Under Model Uncertainty, Singapore National Research Foundation (NRF) Fellowship ($2.29M)
- (Nov. 2018 - Oct. 2022) Information-Theoretic Methods in Data Science, NUS Early Career Research Award ($500k)
- (Jan. 2018 - Jan. 2021) Theoretical and Algorithmic Advances in Noisy Adaptive Group Testing, NUS Startup Grant ($180k)
Ongoing Research Projects
Some potential research projects that students and post-docs could pursue with me are listed below; this list is far from exhaustive.
1) Information-theoretic limits of learning
The field of information theory was introduced as a means for understanding the fundamental limits of data compression and transmission, and has shaped the design of practical communication systems for decades. This project pursues the emerging perspective that information theory is not only a theory of communication, but a far-reaching theory of data benefiting diverse statistical inference and learning problems such as estimation, prediction, and optimization. This perspective leads to principled mathematical approaches to certifying the near-optimality of practical algorithms, and steering practical research towards where the greatest improvements are possible.
- Limits on Support Recovery with Probabilistic Models: An Information-Theoretic Framework
- A Distribution Testing Approach to Clustering Distributions
- Information-Theoretic Lower Bounds for Compressive Sensing with Generative Models
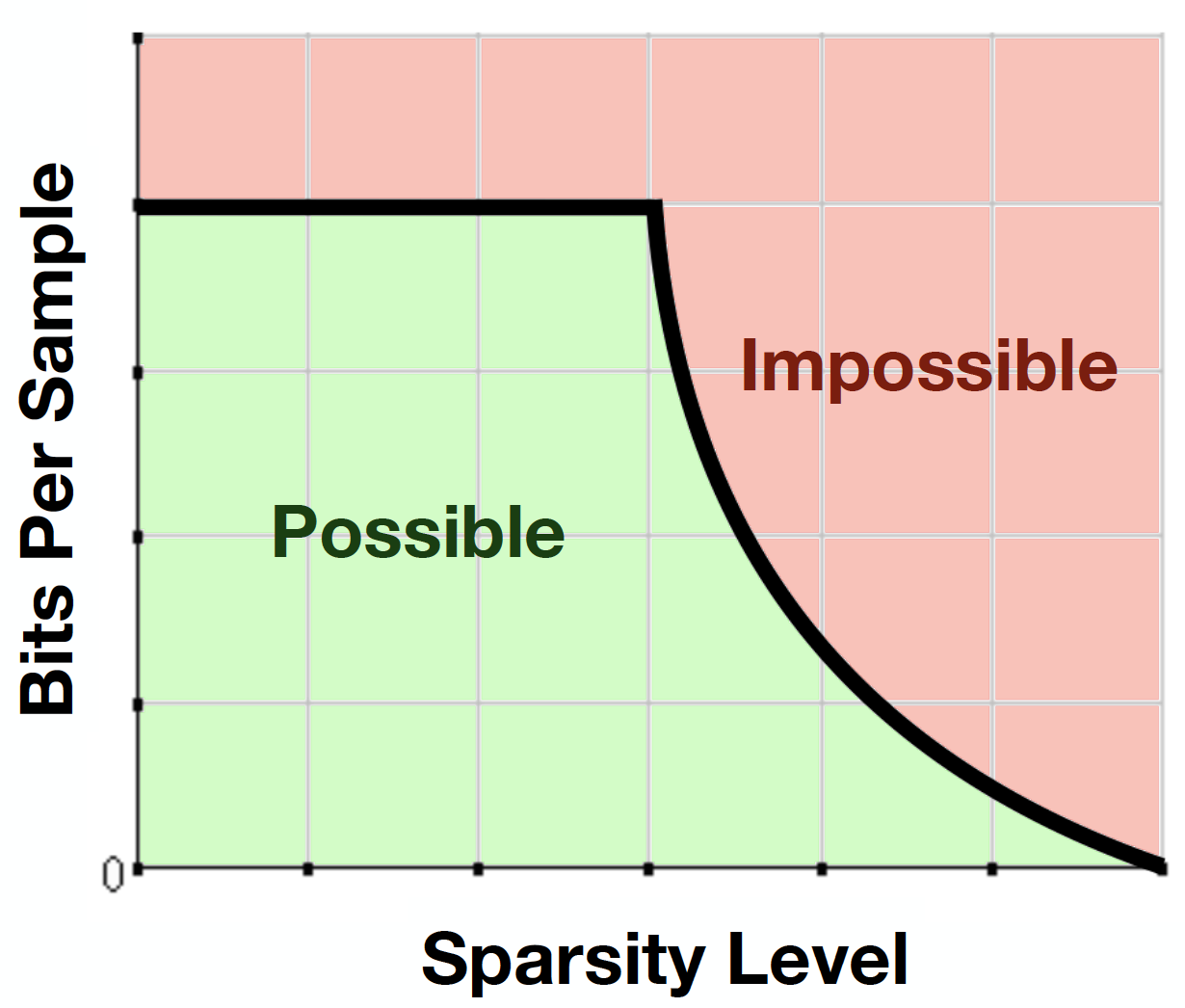
2) Communication-constrained statistical learning
Communication constraints often pose a significant bottleneck in systems involving multiple agents, sensors that send information to a server, and so on. This can significantly complicate statistical learning tasks such as estimation and optimization, as the data samples of interest are no longer observed directly, and the information received may be highly noisy or incomplete. This project seeks to devise learning protocols in which information exchange is carefully designed with communication constraints at the forefront, with an emphasis on rigorous theoretical guarantees on the near-optimality of the trade-off between communication cost and learning performance.

- Sequential 1-bit Mean Estimation with Near-Optimal Sample Complexity
- Optimal Rates of Teaching and Learning Under Uncertainty
- Communication-Constrained Bandits under Additive Gaussian Noise
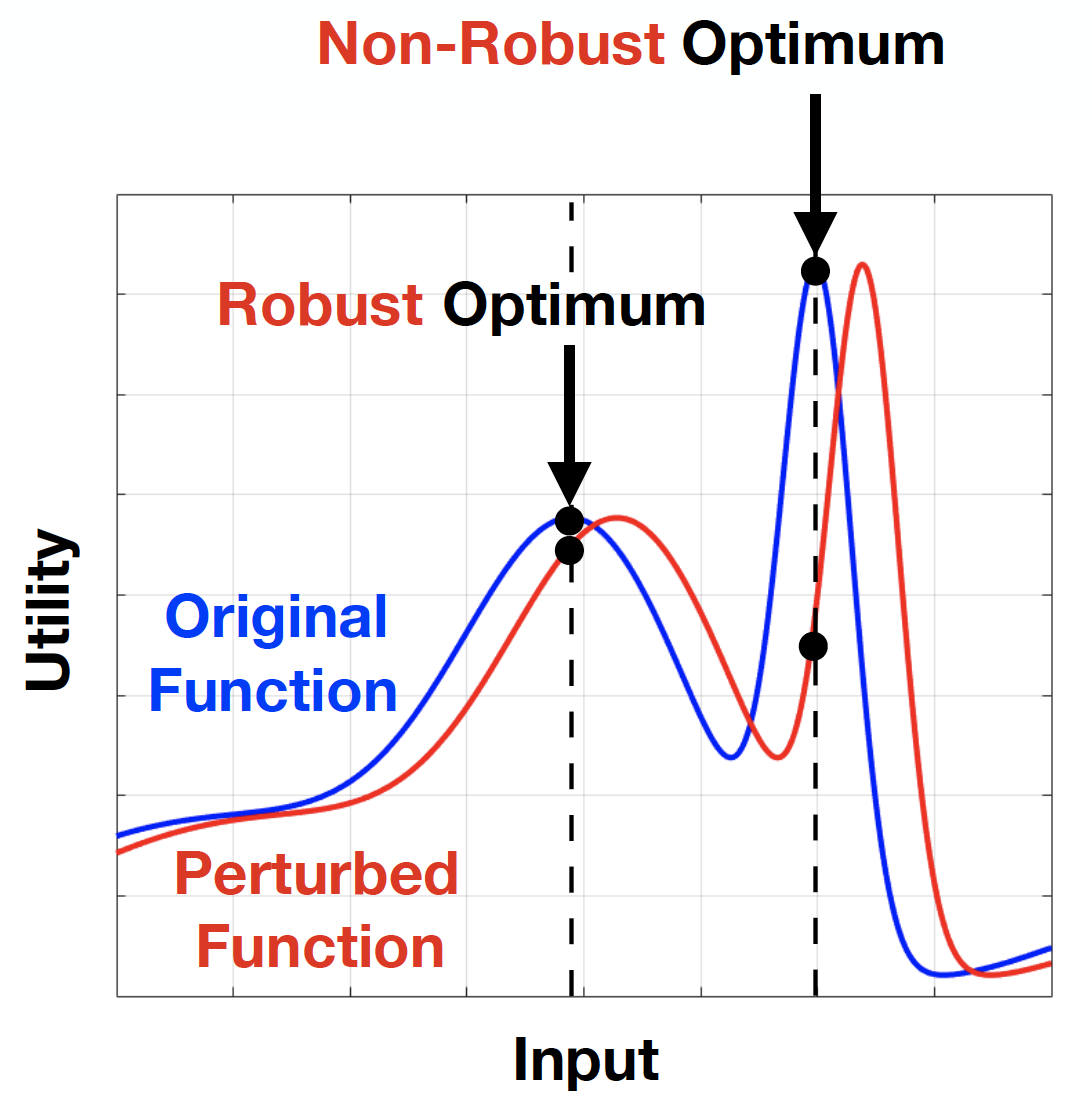
3) Robust statistical learning
Robustness requirements pose many of the most important unsolved challenges in modern machine learning, arising from sources of uncertainty such as mismatched modeling assumptions, corrupted data, and the presence of adversaries. For instance, large distributed learning systems must be able to deal with individual node failures, robotics tasks learned in a simulated environment should be designed to degrade as little as possible when transferred to a real environment, and robustness against adversarial attacks remains a considerable unsolved challenge in deep learning, just to name a few examples. This project seeks to better understand some of the most practically pertinent sources of uncertainty and develop new algorithms that are robust in the face of this uncertainty, with rigorous guarantees.
- Improved Regret Bounds for Linear Bandits with Heavy-Tailed Rewards
- Adversarially Robust Optimization with Gaussian Processes
- Stochastic Linear Bandits Robust to Adversarial Attacks
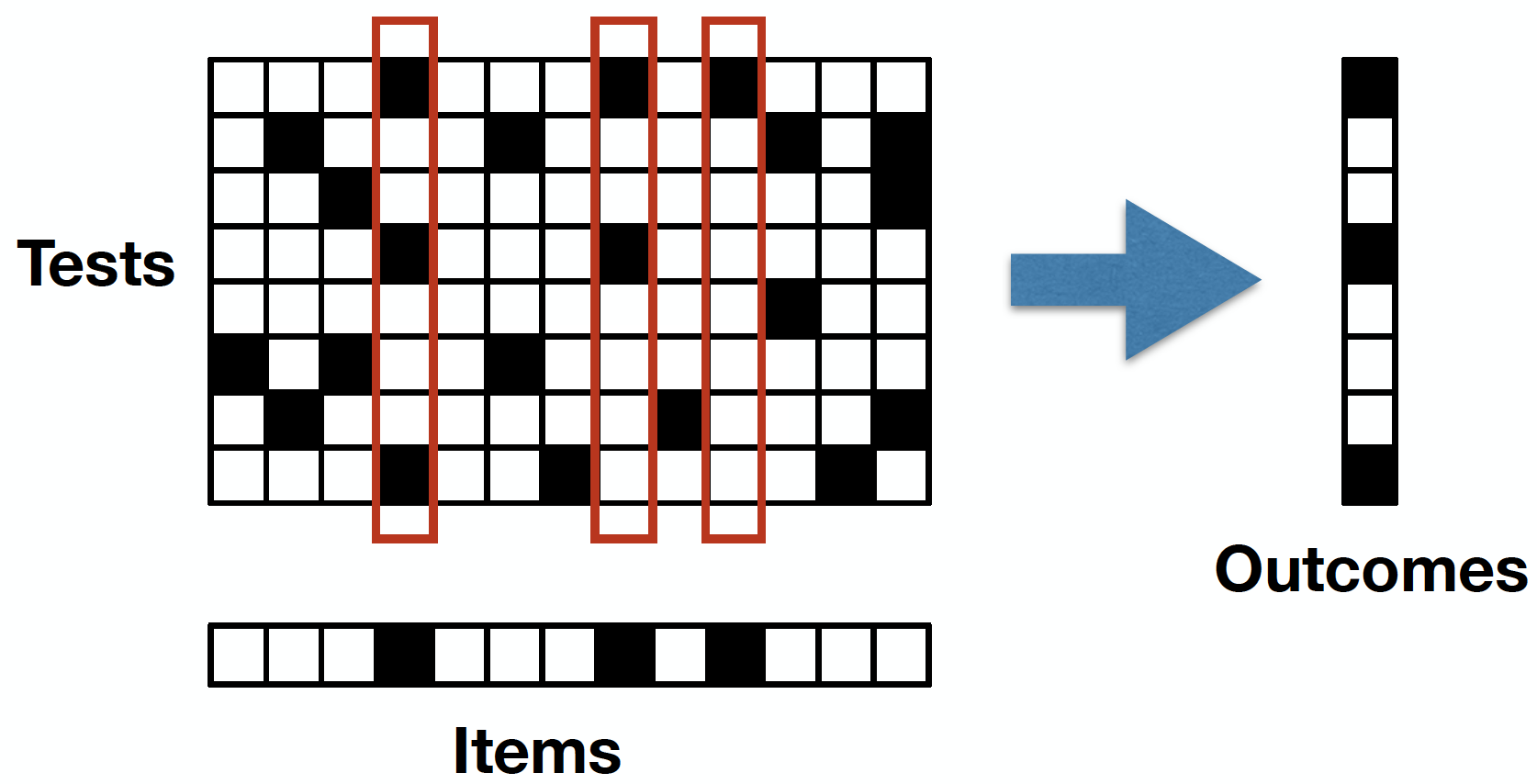
4) Theory and algorithms for group testing
Group testing is a classical sparse estimation problem that seeks to identify "defective" items by testing groups of items in pools, with recent applications including database systems, communication protocols, and COVID-19 testing. A recent line of works has led to significant advances in the theory of group testing, including the development of precise performance limits and practical algorithms for attaining them. This project seeks to push these advances further towards more challenging settings that better account for crucial practical phenomena, including noisy outcomes, testing constraints, prior information, and non-binary measurements.
- Group Testing: An Information Theory Perspective
- Exact Thresholds for Noisy Non-Adaptive Group Testing
- Noisy Adaptive Group Testing: Bounds and Algorithms
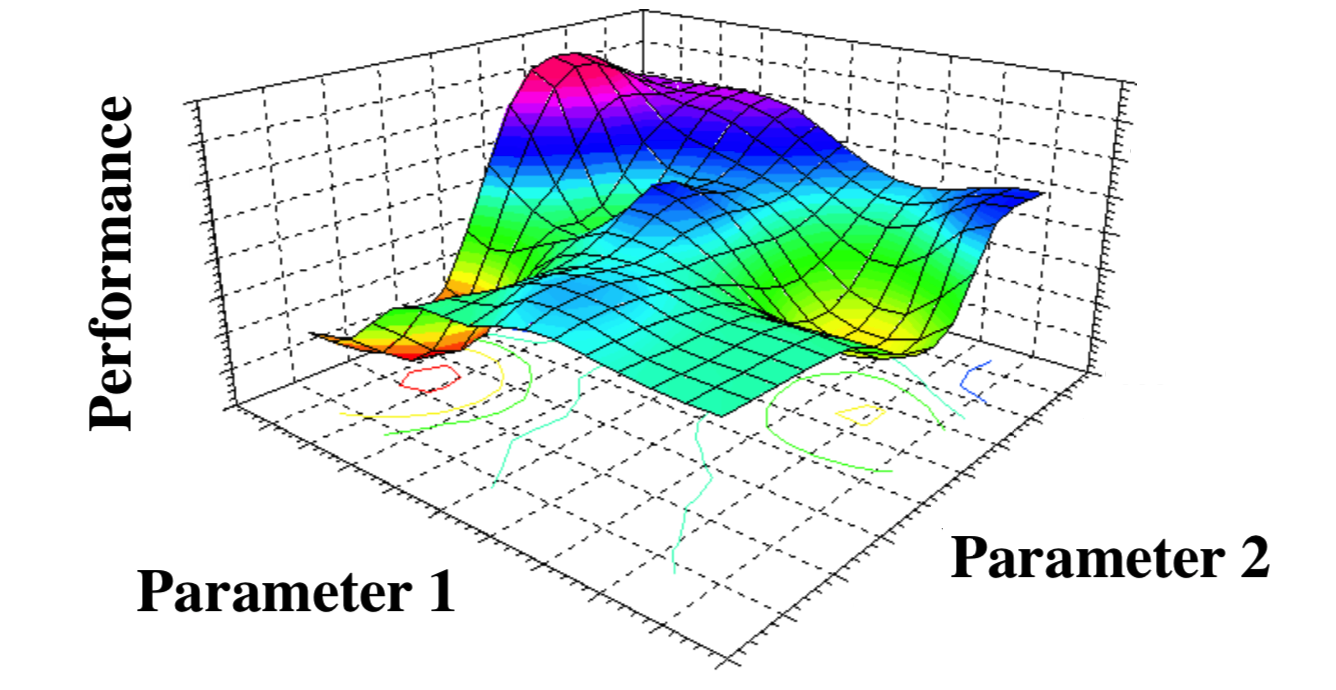
5) Theory and algorithms for Bayesian optimization
Bayesian optimization (BO) has recently emerged as a versatile tool for optimizing "black-box" functions, with particular success in automating machine learning algorithms by learning a good set of hyperparameters (e.g., used in the famous AlphaGo program), as well as other applications such as robotics and materials design. A widespread modeling assumption in BO is that the function is well-approximated by a Gaussian process, whose smoothness properties are dictated by a kernel function. This project seeks to advance the current state-of-the-art theory and algorithms for BO with an emphasis on practical variations that remain lesser-understood, including model misspecification, adversarial corruptions, and high dimensionality.