Massively Parallel Aggregation in Dynamic Networks

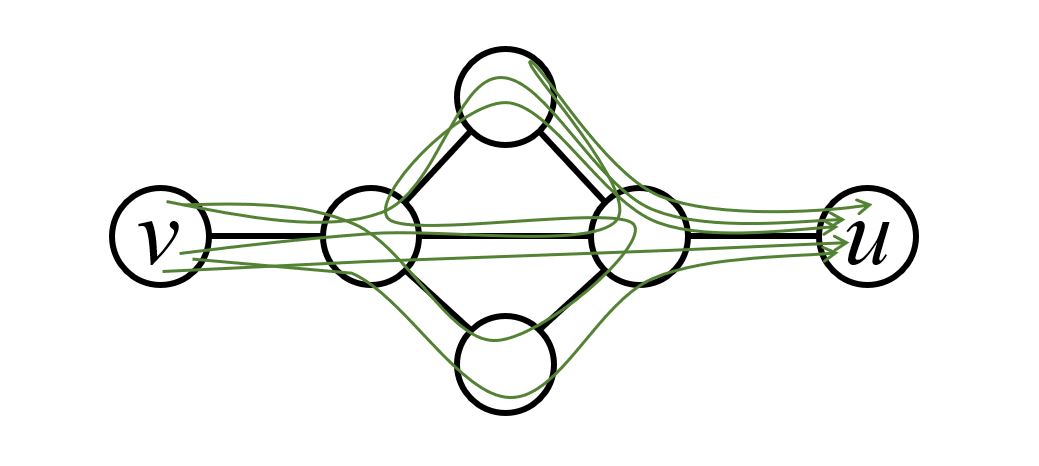
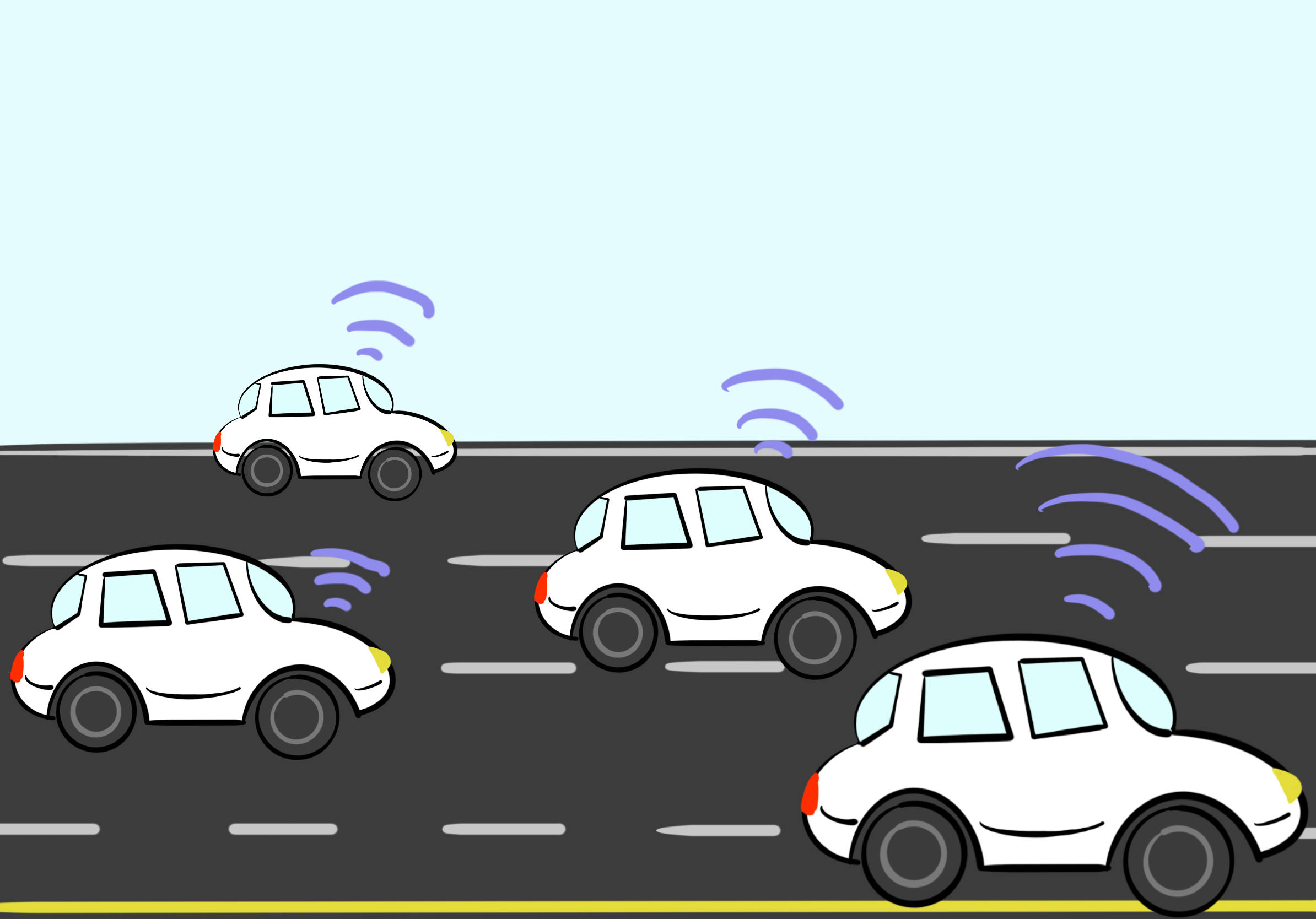
1. Background on dynamic networks

Imagine a futuristic scenario with many smart vehicles on the road. Each smart vehicle can directly communicate with near-by vehicles using wireless communication, as long as they are within the radio range of each other. This essentially gives us a computer network with a certain topology. Interestingly, the topology of this network can change over time, as vehicles keep moving in and out of each other's radio range. Such networks are hence called dynamic networks. Because of the continuous topology changes in such dynamic networks, even basic problems (such as counting the number of nodes in the network) become challenging to solve.

2. Our work: Obtaining sublinear algorithms in dynamic networks

In this research work, we have invented the very first sublinear-complexity algorithms for solving a range of basic problems (such as counting the total number of nodes) in such networks. Our algorithms are based on the key novel idea of massively parallel aggregation. For example, when we want to send a numerical value from a node v to a node u, we split the value evenly across all possible paths (of at most a certain length) from v to u. Note that there can be an exponential number of such paths. We show that such splitting helps to constrain the damage caused by potential topology changes, which eventually leads to algorithm with sublinear time complexity. At the same time, somewhat surprisingly, we also find an efficient way to "implement" such a mechanism with proper data structures, despite the exponential number of paths involved.

For more details, please see: