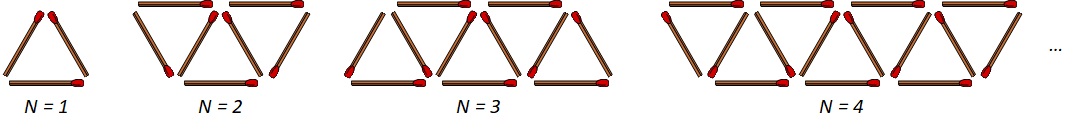Problem Solving with Sequence
Problem Set
The following problem sets are intended for practice.
Attempt these on your own.
Donut
??? example "Problem"
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | ### Problem Description
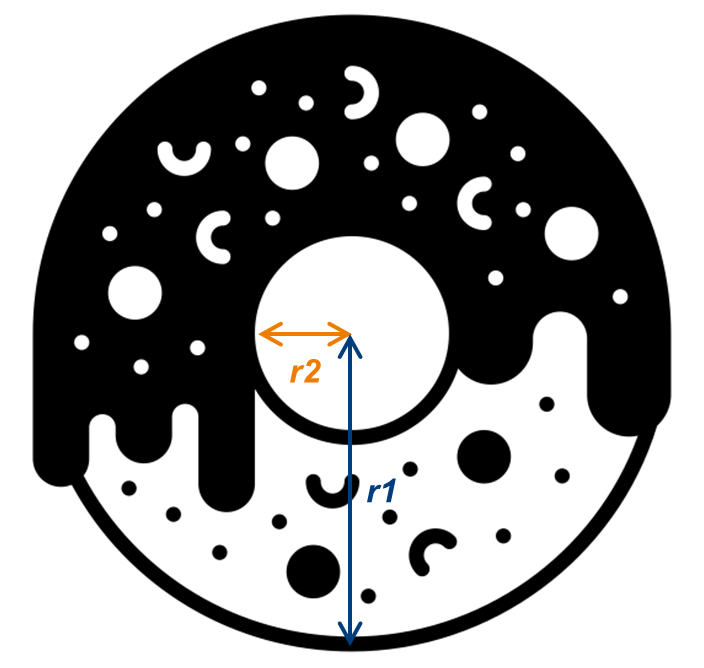
Consider a donut of height `#!py3 h` such that the radius is `#!py3 r1` and the center hole has a radius of `#!py3 r2`.
We let `#!py3 r1 > r2` because the hole cannot be bigger than the donut!
Recap that the are of a circle of radius $r$ is given by the formula below.
$$ A = \pi r^2 $$
We let $\pi$ to be 3.1415 for simplicity.
Afterall, we do not need high precision for our donuts, we enjoy it anyway.
Now, the volume of the donut should be the area times height.
### Task
Write Python code to compute and print the volume of the donut.
We assume that the donut is more like a cylinder so that the formula for the volume above is valid.
### Assumptions
- `#!py3 0 < r2 < r1`
- `#!py3 0 < h`
- `#!py3 h`, `#!py3 r1`, and `#!py3 r2` are already initialized.
|
??? hints "Hints"
??? hint "Hint #1"
=== "Hint"
Can you compute the area of the donut if there is no hole (i.e., assume the hole is filled)?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 | === "Answer"
```py
a1 = 3.1415 * r1 * r1
```
??? hint "Hint #2"
=== "Hint"
Can you compute the area of the hole?
=== "Answer"
```py
a2 = 3.1415 * r2 * r2
```
??? hint "Hint #3"
=== "Hint"
Given area of donut without hole (_i.e.,_ assume the hole is filled) and area of hole, can you compute the area of donut?
=== "Answer"
Let `#!py3 a1` be area of donut without hole (_i.e.,_ assume the hole is filled) and `#!py3 a2` be the area of the hole.
```py
donut_area = a1 - a2
```
??? hint "Hint #4"
=== "Hint"
Given the area of donut, can you compute the volume?
=== "Answer"
Assuming `#!py3 donut_area` is the area of the donut.
```py
volume = donut_area * h
```
??? success "Possible Solution"
```py
# Assume h, r1, and r2 are initialized
a1 = 3.1415 * r1 * r1
a2 = 3.1415 * r2 * r2
donut_area = a1 - a2
volume = donut_area * h
print(volume)
```
|
Cartesian Distance
??? example "Problem"

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | ### Problem Description
We can represent a point in a Cartesian coordinate with two values.
One value represents the position in the x-coordinate and another value represents the position in the y-coordinate.
This is written as $(x, y)$.
For instance, the red point is at (-3, 1) and the green point is at (2, 3).
Given two points $p_1 = (x_1, y_1)$ and $p_2 = (x_2, y_2)$, the distance between them can be computed with the following formula.
$$ d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$
### Task
Write Python code to compute and print the distance between two points represented by (`#!py3 x1`, `#!py3 y1`) and (`#!py3 x2`, `#!py3 y2`).
### Assumptions
- `#!py3 x1`, `#!py3 x2`, `#!py3 y1`, and `#!py3 y2` are integers.
- `#!py3 x1`, `#!py3 x2`, `#!py3 y1`, and `#!py3 y2` are already initialized.
|
??? hints "Hints"
??? hint "Hint #1"
=== "Hint"
First step is to compute \(x_1 - x_2\).
Also compute \(y_1 - y_2\).
What is the expression?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | === "Answer"
```py
dx = x1 - x2
dy = y1 - y2
```
??? hint "Hint #2"
=== "Hint"
How do you compute the square of a value?
=== "Answer"
Two possibilities:
```py
dx * dx
```
```py
dy ** 2
```
??? hint "Hint #3"
=== "Hint"
How do you compute the square root of a value?
=== "Answer"
```py
v ** (0.5)
```
??? success "Possible Solution"
```py
dx = x1 - x2
dy = y1 - y2
dist = (dx * dx + dy * dy) ** 0.5
print(dist)
```
|
Matchstick
??? example "Problem"
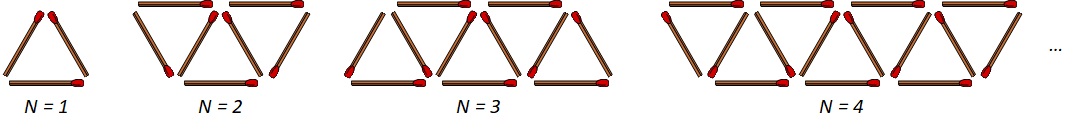
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | ### Problem Description
We want to create a pattern using matchstick as shown above.
The pattern for a given $N$ is created by first creating a pattern for $N - 1$ and then we add 2 additional triangles on the sides.
### Task
Write Python code to compute and print the number of matchstick needed for a given $N$.
The initial value for $N$ is given in the variable `#!py3 n`.
### Assumptions
- `#!py3 0 < n`
|
??? hints "Hints"
??? hint "Hint #1"
=== "Hint"
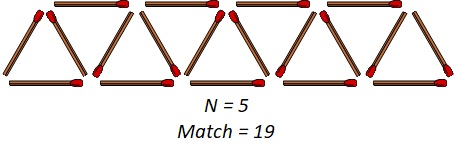
Can you create the pattern for \(N = 5\)?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93 | === "Answer"
{ width="300px" }
??? hint "Hint #2"
=== "Hint"
| n | match | | | |
|---|-------|----|----|----|
| 1 | 3 | | | |
| 2 | 7 | | | |
| 3 | 11 | | | |
| 4 | 15 | | | |
| : | : | | | |
| n | m1 | | | |
Can you find the formula?
Formulate $m1$ in terms of $n$.
You can use the table above.
=== "m1"
| n | match | m1 | | |
|---|-------|----|----|----|
| 1 | 3 | 3 = 3 + 0 | | |
| 2 | 7 | 7 = 3 + 4 | | |
| 3 | 11 | 11 = 3 + 8 | | |
| 4 | 15 | 15 = 3 + 12 | | |
| : | : | : | | |
| n | m1 | m1 = 3 + m2 | | |
Formulate $m2$ in terms of $n$.
=== "m2"
| n | match | m1 | m2 | |
|---|-------|----|----|----|
| 1 | 3 | 3 = 3 + 0 | 0 = 0 * 4 | |
| 2 | 7 | 7 = 3 + 4 | 4 = 1 * 4 | |
| 3 | 11 | 11 = 3 + 8 | 8 = 2 * 4 | |
| 4 | 15 | 15 = 3 + 12 | 12 = 3 * 4 | |
| : | : | : | : | |
| n | m1 | m1 = 3 + m2 | m2 = m3 * 4 | |
Formulate $m3$ in terms of $n$.
=== "m3"
| n | match | m1 | m2 | m3 |
|---|-------|----|----|----|
| 1 | 3 | 3 = 3 + 0 | 0 = 0 * 4 | 0 = 1 - 1 |
| 2 | 7 | 7 = 3 + 4 | 4 = 1 * 4 | 1 = 2 - 1 |
| 3 | 11 | 11 = 3 + 8 | 8 = 2 * 4 | 2 = 3 - 1 |
| 4 | 15 | 15 = 3 + 12 | 12 = 3 * 4 | 3 = 4 - 1 |
| : | : | : | : | : |
| n | m1 | m1 = 3 + m2 | m2 = m3 * 4 | m3 = n - 1 |
Does it work for $n = 5$?
??? success "Possible Solution"
```py
# Assume n is initialized
m3 = n - 1
m2 = m3 * 4
m1 = 3 + m2
print(m1)
```
Can you convert this into a single line?
=== "Copy m3"
```py
# Assume n is initialized
# m3 is copied
m2 = (n - 1) * 4
m1 = 3 + m2
print(m1)
```
=== "Copy m2"
```py
# Assume n is initialized
# m3 is copied
# m2 is copied
m1 = 3 + ((n - 1) * 4)
print(m1)
```
=== "Copy m1"
```py
# Assume n is initialized
# m3 is copied
# m2 is copied
# m1 is copied
print(3 + ((n - 1) * 4))
```
This process can also be done in _reverse_.
|