Summary
Values
Consider 3-bit numbers. The table below shows the comparison for the different representation.
| Values | Sign-and-Magnitude | 1s Complement | 2s Complement | Excess-4 | Excess-3 |
|---|---|---|---|---|---|
| -4 | - | - | 100 | 000 | |
| -3 | 111 | 100 | 101 | 001 | 000 |
| -2 | 110 | 101 | 110 | 010 | 001 |
| -1 | 101 | 110 | 111 | 011 | 010 |
| -0 | 100 | 111 | |||
| +0 | 000 | 000 | 000 | 100 | 011 |
| +1 | 001 | 001 | 001 | 101 | 100 |
| +2 | 010 | 010 | 010 | 110 | 101 |
| +3 | 011 | 011 | 011 | 111 | 110 |
| +4 | 111 |
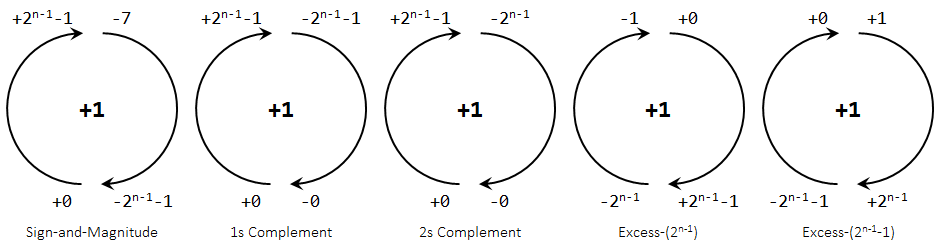
As we keep on adding one to the representation, starting from 000...00, the values that we will encounter can be summarised as a circle. The circle should be read from the bottom. Making a step in clockwise direction adds 1 to the representation. We assume an arbitrary n-bit numbers and truncate the result back to n-bit.
You can click on the header on the table above to change the ordering and verify the circles below.
Operations
We use "-" to indicate that the operation is too complex to describe in a table. However, it does not mean that we cannot perform the operation.
| Operations | Sign-and-Magnitude | 1s Complement | 2s Complement | Excess-N |
|---|---|---|---|---|
| Negation | Invert left-most bit | Invert all bits | Invert all bits Add 1 |
- |
| Addition | - | Binary addition Add Carry1 Truncate2 |
Binary addition Truncate2 |
- |
| Subtraction | A + (-B)3 | |||
| Comparison | - | - | - | Binary comparison |
For sign-and-magnitude, 1s complement and 2s complement, negation is a bidirectional process. Consider an 8-bit number.
- (23)10 = 00010111
- Invert left-most bit: 10010111 ⇒ (-23)10
- (-23)10 = 10010111
- Invert left-most bit: 00010111 ⇒ (23)10
- (23)10 = 00010111
- Invert all bit: 11101000 ⇒ (-23)10
- (-23)10 = 11101000
- Flip first bit: 00010111 ⇒ (23)10
- (23)10 = 00010111
- Invert all bit: 11101000
- Add 1: 11101001 ⇒ (-23)10
- (-23)10 = 11101001
- Invert all bit: 00010110
- Add 1: 00010111 ⇒ (23)10
Formula
For 1s complement and 2s complement, we can also use a formula to compute a number for which the binary representation will give us the correct representation for 1s complement or 2s complement.
| Number of Bits | 1s Complement | 2s Complement |
|---|---|---|
| n | -x=2n-x-1 | -x=2n-x |
Note that the formula only works for whole numbers. However, we can extend this in two different directions.
Radix Complement
The first extension is to abstract the radix (i.e., the base) into any number. Since we have two kinds of complements (i.e., 1s complement and 2s complement for base 2), the extension to any radix may cause confusion. So, they are actually called diminished radix complement and radix complement respectively. Alternatively, they are called (b-1)s complement and (b)s complement respectively.
| Number of Digits | Radix | (b-1)s Complement | (b)s Complement |
|---|---|---|---|
| n | b | -x = bn-x-1 | -x = bn-x |
Example
Consider the number (43)10. We can express this in 5-trit4 number as (01121)3. The negations are:
- (b-1)s Complement: 21101
- -43 = 35-43-1 = 199
- (199)10 = (21101)3
- (b)s Complement: 21102
- -43 = 35-43 = 200
- (200)10 = (21102)3
Quick Quiz
- What is the negation of (2100)10 in (b)s complement where b = 10 using 5 digits?
- Since 2s complement allows us to perform addition as simple binary addition, can you do that for 10s complement? If so, can you show the result for 2100 - 1010 using 10s complement with 5 digits?
-
(97900)10s
Steps
- -2100 = 105-2100 = 97900
- already in base 10
-
(01090)10s
Steps
- -1010 = 105-1010 = 98990
- 2100 - 1010 = 2100 + 98990 = 101090
- Truncate the result: 01090
This is simply the case of "borrowing" from the digits to the left taken to the extreme.
Fractions
The second extension is to extend the idea of complement to fractions. The basic idea is simply to first remove the dot, convert, then add back the dot into the correct location.
Immediately, that poses problem for the formula of 1s complement. Here, we subtract 1 in -x=2n-x-1 assuming that the smallest number is 1. This is correct if we remove the dot. But if we wish to find a formula that takes into account the dot, we cannot use 1. Instead, we need to use the smallest number given the dot. So, we specify two number of bits: the whole number (n) and the fraction f. The smallest tnumber can then be calculated as 2-f. Luckily, negation by inverting all bits still applies!
As for the case of 2s complement, negation by inverting all bits and adding 1 does not work for the same reason that 1 was assumed to be the smallest number. But again, we can simply find the smallest number using the same method as in 1s complement and add that instead. Luckily, the formula for 2s complement is unchanged!
| Whole Number of Bits | Fractional Bits | 1s Complement | 2s Complement |
|---|---|---|---|
| n | f | -x=2n-x-2-f | -x=2n-x |
| Invert all bits | Invert all bits Add $2-f |
Example
Negate (5.25)10 in 1. 1s complement using 4-bit whole number and 2-bit fraction 2. 2s complement using 4-bit whole number and 2-bit fraction
(1010.10)1s
- Find the binary representation of (5.25)10: (0101.01)2
- Invert all the bits: (1010.10)1s
- Find the "equivalent" number: -5.25 = 24-5.25-2-2 = 16-5.25-0.25 = 10.5
- Find the binary representation of (10.5)10: (1010.10)2
- Change the base: (1010.10)1s
(1010.11)2s
- Find the binary representation of (5.25)10: (0101.01)2
- Invert all the bits: (1010.10)1s
- Add 2-f = 2-2 = (0.01)2: (1010.11)2s
- Find the "equivalent" number: -5.25 = 24-5.25-2-2 = 10.75
- Find the binary representation of (10.75)10: (1010.11)2
Quick Quiz
- Negate (111000.101)2 in 1s complement using 6-bit whole number and 3-bit fraction.
- Negate (111000.101)2 in 2s complement using 6-bit whole number and 3-bit fraction.
- (000111.010)1s
- (000111.011)2s
Past Year Exam's Question
Consider the following C code
| PastYearQn.c | |
|---|---|
1 2 3 4 5 | |
What is the output of the code above when run on sunfire?
n = -2147483546
Explanation
C uses 2s complement number system.
Additionally, int is a 32-bit number, so the largest number is 231-1 = 2147483647.
We can trace the execution as follows:
| Iteration | n = |
Comment |
|---|---|---|
| pre | 2147483640 |
Before the for-loop |
| 1 | 2147483641 |
|
| 2 | 2147483642 |
|
| 3 | 2147483643 |
|
| 4 | 2147483644 |
|
| 5 | 2147483645 |
|
| 6 | 2147483646 |
|
| 7 | 2147483647 |
Max int value: 0111 ... 1111 |
| 8 | -2147483648 |
Min int value: 1000 ... 0000 |
| 9 | -2147483647 |
|
| 10 | -2147483646 |
|
| post | -2147483646 |
After the for-loop |
Exercises
Exercise
Represent -5510 using 8-bits in the following representation:
- Sign-and-Magnitude.
- 1s Complement.
- 2s Complement.
- Excess-128.
First, note that 5510 = 001101112.
- 10110111sm
- Simply flip the first bit to 1.
- 110010001s
- Simply flip all the bits.
- 110010012s
- From answer to question 2, we add 1.
- 01001001e-128
- 128-55 = 73
- 7310 = 010010012
-
Adding carry is really just a short-hand for checking if we have crossed the redundant 0. Since by crossing the redundant 0 we require an additional bit to represent the number, that additional bit is going to be 1. So, just add this carry bit regardless. ↩
-
There is an additional check for overflow. However, it is only useful if we want to know that an overflow occurs. In C, the overflow can occur silently. ↩↩
-
At this point, we assume that we can negate a number (-B) and we can add two numbers A + (...). ↩
-
Ternary digits ↩